神经网络简介
最近听取了Batman成员关于神经网络的讲座,十分精彩,学习到了不少东西,担心遗忘,在这里做个总结与回顾。
阅读本篇博文,可能需要掌握机器学习的一些基础知识。我在本科阶段选修了《数据仓库与数据挖掘》,对相关领域有所了解就足够了。
概述
定义
首先引用西瓜书对于神经网络的定义:神经网络是由具有适应性的简单单元组成的广泛并行互联的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。
定义中提及的简单单元常被称为神经元。生物的神经元是这样的:接收来自$n$个其它神经元传递过来的输入信号,加权后与阈值比较,通过一个阶跃函数处理产生自己的输出。在机器学习领域中,神经元也是类似的,只不过这里用激活函数代替阶跃函数。激活函数多种多样,常见的有sigmoid函数$f(z)=\frac{1}{1+e^{-z}}$。此外,还增加了截距使得直线可平移,截距项被称为偏置节点。
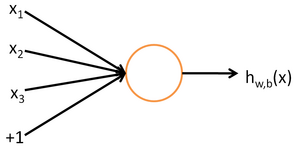
这个神经元是一个以$x_1,x_2,x_3$及截距$+1$为输入值的运算单元,输出为$h_{W,b}(x)=f(W^T x)=f(\sum_{i=1}^3 W_i x_i+b)$。
神经网络就是将许多个单一神经元按照一定的层次结构连接在一起,一个神经元的输出就可以是另一个神经元的输入。例如,下图就是一个简单的神经网络。
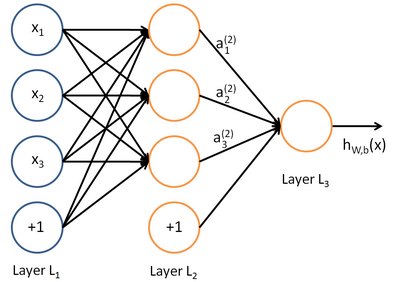
神经网络最左边的一层叫做输入层,最右的一层叫做输出层。中间所有节点组成的层叫做隐藏层。上图中,只有一个隐藏层和一个输出节点,然而它们也可以有多个。
公式表达
下面给出数学公式表达形式。用$n_l$表示网络的层数,$L_l$表示第$l$层。例如,图中$n_l=3$,输出层是$L_{n_l}$即为$L_{3}$。设$W_{ij}^{(l)}$是第$l$层第$j$单元与第$l+1$层第$i$单元之间的连接权重,$b_{i}^{(l)}$是第$l+1$层第$i$单元的偏置项,$s_l$为第$l$层的节点数(不含偏置节点)。
我们用$a_{i}^{(l)}$表示第$l$层第$i$单元的输出值。当$l=1$时,$a_{i}^1=x_i$。于是,对于给定参数集合$W,b$,神经网络可以按照函数$h_{W,b}(x)$计算输出结果。本例神经网络的计算步骤如图。
$a_1^{(2)}=f(W_{11}^{(1)}x_1+W_{12}^{(1)}x_2+W_{13}^{(1)}x_3+b_1^{(1)})$
$a_2^{(2)}=f(W_{21}^{(1)}x_1+W_{22}^{(1)}x_2+W_{23}^{(1)}x_3+b_2^{(1)})$
$a_3^{(2)}=f(W_{31}^{(1)}x_1+W_{32}^{(1)}x_2+W_{33}^{(1)}x_3+b_3^{(1)})$
$h_{W,b}(x)=a_1^{(3)}=f(W_{11}^{(2)}a_1^{(2)}+W_{12}^{(2)}a_2^{(2)}+W_{13}^{(2)}a_3^{(2)}+b_1^{(2)})$
我们用$z_i^{(l)}$表示第$l$层第$i$单元输入的加权和(包括偏置单元),例如$z_i^{(2)} = \sum_{j=1}^n W^{(1)}_{ij} x_j + b^{(1)}_i$。这样就可以采用下面这种更简洁的表示法。将激活函数$f(\cdot)$扩展为用向量(分量的形式)来表示,即$f([z_1, z_2, z_3]) = [f(z_1), f(z_2), f(z_3)]$,则上面的等式可以表示为:
$z^{(2)}=W^{(1)}x+b^{(1)}$
$a^{(2)}=f(z^{(2)})$
$z^{(3)}=W^{(2)}a^{(2)}+b^{(2)}$
上面的计算步骤叫作前向传播。之前用$a^{(1)} = x$表示输入层的激活值,那么给定第$l$层的激活值$a^{(l)}$后,第 $l+1$ 层的激活值$a^{(l+1)}$就可以按照下面步骤计算得到:
$z^{(l+1)}=W^{(l)}a^{(l)}+b^{(l)}$
$a^{(l+1)}=f(z^{(l+1)})$
可以看出,这些参数实际上就是一个个矩阵。使用矩阵-向量的形式,可以利用线性代数的知识,快速求解、证明神经网络的一些问题。
反向传导算法
显然,多层神经网络的学习能力比单层网络强得多,实际上也是如此。反向传导算法(error BackPropagation,简称BP,又译为误差逆传播算法)就是一个训练多层神经网络的优秀算法。其基本思想是,学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时,输入样本从输入层传入,经各隐藏层逐层处理后,传向输出层。若输出层的实际输出与期望的输出不符,则转入误差的反向传播阶段。误差反传是将输出误差以某种形式通过隐藏层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。这种信号正向传播与误差反向传播的各层权值调整过程,是周而复始地进行的。权值不断调整的过程,也就是网络的学习训练过程。此过程一直进行到网络输出的误差减少到可接受的程度,或进行到预先设定的学习次数为止。
梯度下降法
BP算法基于梯度下降(gradient descent)策略。梯度下降法常用来递归性地逼近最小偏差模型,沿梯度的方向逼近极小值。下图给出一个函数图象作为示例。
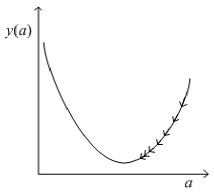
梯度下降法沿右边箭头方向,逐渐逼近函数的极小值。本例中,这个极小值就是函数的最小值。
梯度下降法的迭代公式可以表示为$a_{k+1}=a_k+\rho_k \bar s_{(k)}$,其中$\bar s_{(k)}$代表梯度负方向,$\rho_k$ 表示梯度方向上的搜索步长。梯度方向我们可以通过对函数求导得到。步长的确定比较麻烦,太大了的话可能会发散,太小收敛速度又太慢,一般确定步长的方法是由线性搜索算法来确定,即把下一个点的坐标看做是$a_{k+1}$的函数,然后求满足$f(a_{k+1})$的最小值即可。
一般情况下,导数值为0则说明达到极值点。采用梯度下降算法进行最优化求解时,算法迭代的终止条件是梯度向量的幅值接近0即可,可以设置一个非常小的常数作为阈值。
公式表达
代价函数
假设我们有一个固定样本集${ (x^{(1)}, y^{(1)}), \ldots, (x^{(m)}, y^{(m)}) }$,它包含$m$个样例。我们可以用批量梯度下降法来求解神经网络。具体来讲,对于单个样例$(x,y)$,其代价函数为:
$J(W,b; x,y) = \frac{1}{2} \left| h_{W,b}(x) - y \right|^2$
这是一个(二分之一的)方差代价函数。使用二分之一的原因是后面求导的方便。给定一个包含$m$个样例的数据集,我们可以定义整体代价函数为:
$J(W,b) = \left[ \frac{1}{m} \sum_{i=1}^m J(W,b;x^{(i)},y^{(i)}) \right] + \frac{\lambda}{2} \sum_{l=1}^{n_l-1} ; \sum_{i=1}^{s_l} ; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2 $
$= \left[ \frac{1}{m} \sum_{i=1}^m \left( \frac{1}{2} \left| h_{W,b}(x^{(i)}) - y^{(i)} \right|^2 \right) \right] + \frac{\lambda}{2} \sum_{l=1}^{n_l-1} ; \sum_{i=1}^{s_l} ; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2$
以上关于$J(W,b)$定义中的第一项是一个均方差项。第二项是一个规则化项(也叫权重衰减项),其目的是减小权重的幅度,防止过度拟合。$\lambda$叫做权重衰减参数,用于控制公式中两项的相对重要性,需要算法工程师根据经验调整。使用二分之一的原因同样是后面求导的方便。
以上的代价函数经常被用于分类和回归问题。在分类问题中,我们用$y = 0$或$1$来代表两种类型的标签。对于回归问题,我们首先要变换输出值域$y$,以保证其范围为$[0,1]$。值域应根据激活函数确定,此处使用$[0,1]$是因为sigmoid激活函数的值域为$[0,1]$。
我们的目标是针对参数$W$和$b$来求其函数$J(W,b)$的最小值。为了求解神经网络,我们需要将每一个参数$W^{(l)}_{ij}$和$b^{(l)}_i$初始化为一个很小的、接近零的随机值,之后对目标函数使用诸如批量梯度下降法的最优化算法。因为$J(W, b)$是一个非凸函数,梯度下降法很可能会收敛到局部最优解;但是在实际应用中,梯度下降法通常能得到令人满意的结果。
最后,需要再次强调的是,要将参数进行随机初始化,而不是全部置为$0$。如果所有参数都用相同的值作为初始值,那么所有隐藏层单元最终会得到与输入值有关的、相同的函数(也就是说,对于所有$i$,$W^{(1)}_{ij}$都会取相同的值,那么对于任何输入 $x$都会有:$a^{(2)}_1 = a^{(2)}_2 = a^{(2)}_3 = \ldots$)。随机初始化的目的是使对称失效。
梯度下降法中每一次迭代都按照如下公式对参数$W$和$b$进行更新:
$W_{ij}^{(l)} = W_{ij}^{(l)} - \alpha \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b)$
$b_{i}^{(l)} = b_{i}^{(l)} - \alpha \frac{\partial}{\partial b_{i}^{(l)}} J(W,b)$
其中$\alpha$是学习速率。
反向传播算法
公式计算的关键步骤是计算偏导数。下面介绍反向传播算法,它是计算偏导数的一种有效方法。本节内容涉及到许多复杂的数学求解,请耐心阅读。
首先计算$\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y)$和$\frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y)$,这两项是单个样例$(x,y)$的代价函数$J(W,b;x,y)$的偏导数。一旦我们求出该偏导数,就可以推导出整体代价函数$J(W,b)$的偏导数:
$\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) =\left[ \frac{1}{m} \sum_{i=1}^m \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x^{(i)}, y^{(i)}) \right] + \lambda W_{ij}^{(l)}$
$\frac{\partial}{\partial b_{i}^{(l)}} J(W,b) =\frac{1}{m}\sum_{i=1}^m \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x^{(i)}, y^{(i)})$
第一行比第二行多出一项,是因为权重衰减是作用于$W$而不是$b$。
反向传播算法的思路如下:给定样例$(x,y)$,首先进行前向传导运算,计算出网络中所有的激活值,包括$h_{W,b}(x)$的输出值。之后,针对第$l$层的每一个节点$i$,我们计算出其残差$\delta^{(l)}_i$,该残差表明了该节点对最终输出值的残差产生了多少影响。对于最终的输出节点,我们可以直接算出网络产生的激活值与实际值之间的差距,我们将这个差距定义为$\delta^{(n_l)}_i$(第$n_l$层表示输出层)。对于隐藏单元,将基于第$l+1$层节点)残差的加权平均值计算$\delta^{(l)}_i$,这些节点以$a^{(l)}_i$作为输入。
下面是反向传导算法的细节:
进行前馈传导计算,利用前向传导公式,得到$L_2, L_3, \ldots$直到输出层$L_{n_l}$的激活值。
对于第$n_l$层(输出层)的每个输出单元$i$,根据以下公式计算残差:
$\delta_i^{(n_l)} = \frac{\partial}{\partial z_i^{n_l}}J(W,b;x,y)= \frac{\partial}{\partial z_i^{n_l}}\frac{1}{2} \left|y - h_{W,b}(x)\right|^2$
$= \frac{\partial}{\partial z_i^{n_l}}\frac{1}{2} \sum_{j=1}^{S_{n_l}} (y_j-a_j^{(n_l)})^2= \frac{\partial}{\partial z_i^{n_l}}\frac{1}{2} \sum_{j=1}^{S_{n_l}} (y_j-f(z_j^{(n_l)}))^2$
因为$(x^\mu)’=\mu x^{\mu -1}$,根据复合函数求导法则,对上式继续化简有:
$\delta_i^{(n_l)} = - (y_i - f(z_i^{(n_l)})) \cdot f’(z^{(n_l)}_i)= - (y_i - a^{(n_l)}_i) \cdot f’(z^{(n_l)}_i)$对$l = n_l-1, n_l-2, n_l-3, \ldots, 2$的各个层,第$l$层的第$i$个节点的残差计算方法如下:
$\delta_i^{(n_l-1)} =\frac{\partial}{\partial z_i^{n_l-1}}J(W,b;x,y)= \frac{\partial}{\partial z_i^{n_l-1}}\frac{1}{2} \left|y - h_{W,b}(x)\right|^2 = \frac{\partial}{\partial z_i^{n_l-1}}\frac{1}{2} \sum_{j=1}^{S_{n_l}}(y_j-a_j^{(n_l)})^2 $
$= \frac{1}{2} \sum_{j=1}^{S_{n_l}}\frac{\partial}{\partial z_i^{n_l-1}}(y_j-a_j^{(n_l)})^2= \frac{1}{2} \sum_{j=1}^{S_{n_l}}\frac{\partial}{\partial z_i^{n_l-1}}(y_j-f(z_j^{(n_l)}))^2$
因为$z_j^{n_l}=\sum W_{jk}^{n_l-1}f(z_k^{n_l-1})+b$,
$\delta_i^{(n_l-1)} = \sum_{j=1}^{S_{n_l}}-(y_j-f(z_j^{(n_l)})) \cdot \frac{\partial}{\partial z_i^{(n_l-1)}}f(z_j^{(n_l)})$
又因为$\frac{\partial}{\partial z_i^{n_l-1}}f(z_j^{n_l})=\frac{\partial}{\partial z_i^{n_l}} \frac{\partial z_i^{n_l}}{\partial z_i^{n_l-1}} f(z_j^{n_l})$,继续推导,
$\delta_i^{(n_l-1)} = \sum_{j=1}^{S_{n_l}}-(y_j-f(z_j^{(n_l)})) \cdot f’(z_j^{(n_l)}) \cdot \frac{\partial z_j^{(n_l)}}{\partial z_i^{(n_l-1)}}$
$= \sum_{j=1}^{S_{n_l}} \delta_j^{(n_l)} \cdot \frac{\partial z_j^{(n_l)}}{\partial z_i^{n_l-1}}= \sum_{j=1}^{S_{n_l}} \left(\delta_j^{(n_l)} \cdot \frac{\partial}{\partial z_i^{n_l-1}}\sum_{k=1}^{S_{n_l-1}}f(z_k^{n_l-1}) \cdot W_{jk}^{n_l-1}\right)$
$= \sum_{j=1}^{S_{n_l}} \delta_j^{(n_l)} \cdot W_{ji}^{n_l-1} \cdot f’(z_i^{n_l-1})= \left(\sum_{j=1}^{S_{n_l}}W_{ji}^{n_l-1}\delta_j^{(n_l)}\right)f’(z_i^{n_l-1})$
将上式中的$n_l-1$与$n_l$的关系替换为$l$与$l+1$的关系,就可以得到:
$ \delta_i^{(l)} = \left( \sum_{j=1}^{s_{l+1}} W^{(l)}_{ji} \delta^{(l+1)}_j \right) f’(z^{(l)}_i)$
观察到,计算前一层的导数,用到了后一层的导数结果。逐次从后向前求导的过程即为“反向传导”的本意所在。
计算我们需要的偏导数:
$\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y) = a^{(l)}_j \delta_i^{(l+1)}$
$\frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y) = \delta_i^{(l+1)}$
下面用矩阵-向量表示法重写以上算法。上面定义过$f([z_1, z_2, z_3]) = [f(z_1), f(z_2), f(z_3)]$,则有$f’([z_1, z_2, z_3]) = [f’(z_1), f’(z_2), f’(z_3)]$。“$\bullet$”表示向量乘(点乘)。反向传播算法可表示为以下几个步骤:
- 进行前馈传导计算,利用前向传导公式,得到$L_2, L_3, \ldots$直到输出层$L_{n_l}$的激活值。
- 对输出层(第$n_l$层),计算$\delta^{(n_l)}= - (y - a^{(n_l)}) \bullet f’(z^{(n_l)})$。
- 对于$l = n_l-1, n_l-2, n_l-3, \ldots, 2$的各层,计算$\delta^{(l)} = \left((W^{(l)})^T \delta^{(l+1)}\right) \bullet f’(z^{(l)})$
- 计算最终需要的偏导数值:
$\begin{align}
\nabla_{W^{(l)}} J(W,b;x,y) = \delta^{(l+1)} (a^{(l)})^T, \
\nabla_{b^{(l)}} J(W,b;x,y) = \delta^{(l+1)}.
\end{align}$
利用偏导数值,对参数$W$与$b$进行迭代更新,减小代价函数$J(W,b)$的值,即可求解神经网络。