模拟退火算法简介

发表于 更新于

今天整理的算法是一种概率算法，它与我们以前提到过的神经网络关系紧密：可以用于解决神经网络求解最值问题；与神经网络类似，灵感来源于自然科学。下面开始介绍这个有趣的算法。

再论梯度下降法

上一篇有关于神经网络的博文介绍了梯度下降法，它常用来递归性地逼近最小偏差模型，沿梯度的方向逼近极小值。并给了一个这样的函数图象作为示例。

梯度下降示意图

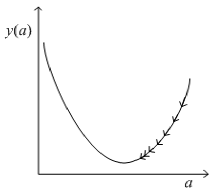
梯度下降法沿右边箭头方向，逐渐逼近函数的极小值。本例中，这个极小值就是函数的最小值。

在这个例子中，一切都非常简单、完美。但是同时也存在着一些不太“完美”的函数，例如把上面的函数略作修改即有下图。

梯度下降的局限性示意图

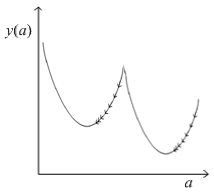
若梯度下降法的起点在左侧，则很容易在第一个极值点结束，终止于局部极小而错过了全局最小。遇到更复杂、极值点更多的函数，梯度下降法的结果可能更差。因此，这一方法具有局限性，很多情况下不能得到理想的结果。因此人们提出了模拟退火算法。

模拟退火算法

背景

与梯度下降法的目的类似，模拟退火算法用来在固定时间内寻求在一个大的搜寻空间内找到的最优解。模拟退火来自冶金学的专有名词退火。退火是将材料加热后再经特定速率冷却，目的是增大晶粒的体积，并且减少晶格中的缺陷。材料中的原子原来会停留在使内能有局部最小值的位置，加热使能量变大，原子会离开原来位置，而随机在其他位置中移动。退火冷却时速度较慢，使得原子有较多可能可以找到内能比原先更低的位置。

其原理也和金属退火的原理近似：我们将热力学的理论套用到统计学上，将搜寻空间内每一点想像成空气内的分子；分子的能量，就是它本身的动能；而搜寻空间内的每一点，也像空气分子一样带有“能量”，以表示该点对命题的合适程度。算法先以搜寻空间内一个任意点作起始：每一步先选择一个“邻居”，然后再计算从现有位置到达“邻居”的概率。

算法

整个算法核心的思路是：搜索到局部最优解后，会以一定概率接受移出局部最优的动作。经过几次类似的移动后，也许会到达一个更优的解。若没有找到更加优秀的解，则次数达到限制后结束算法。

这个概率最常用的是Metropolis准则：若移动后找到了更加优秀的解，则接受这个解；否则，以概率$e^{-\frac{\Delta E}{t}}$接受移动。这里$\Delta E$表示能量差，$t$表示当前温度。即温度越高，越有可能接受移动；温度降低则趋于稳定。

算法的结束调件是：尝试次数用尽，或者温度达到了预先规定的最小值。此时算法给出记录下的最优解。

伪代码

1
2
3
4
5
6
7
8
9
s := s0; e := E (s)                           // 设定目前状态为s0，其能量E (s0)
k := 0                                            // 评估次数k
while k < kmax and e > emax     // 若还有时间（评估次数k还不到kmax）且结果还不够好（能量e不够低）
  sn := neighbour (s)                    //  随机选择临近状态sn
  en := E (sn)                                 //  sn的能量为E (sn)
  if random() < P(e, en, temp(k/kmax)) then  //   决定是否移至临近状态sn
    s := sn; e := en                         //  移至临近状态sn
  k := k + 1                                   //  评估完成，次数k加1
return s

参考文献