决策树与随机森林简介
在数据挖掘与机器学习中,决策树是一种常用的预测模型,树中每个节点表示某个对象,而每个分叉路径则代表某个可能的属性值;随机森林是一个包含多个决策树的分类器,并且其输出的类别是由个别树输出的类别的众数而定。本篇博文按照由浅入深的顺序,依次整理介绍这两种模型相关联的知识。
决策树
基本概念
决策树是一种常用的分类方法。每个决策或事件都可能引出两个或多个事件,导致不同的结果(即分成不同的类别),把这种决策分支画成图形很像一棵树的枝干,故称决策树。当希望针对给定训练数据集进行学习(即监督学习),以对其它数据进行分类时,可以使用决策树。
一个决策树包含一个根节点、若干内部节点与若干叶节点。根节点是分类的起点,叶节点对应具体的决策结果,从根节点到叶节点的路径对应了一个判断序列。下图给出了一个决策树及其对应的数据集。
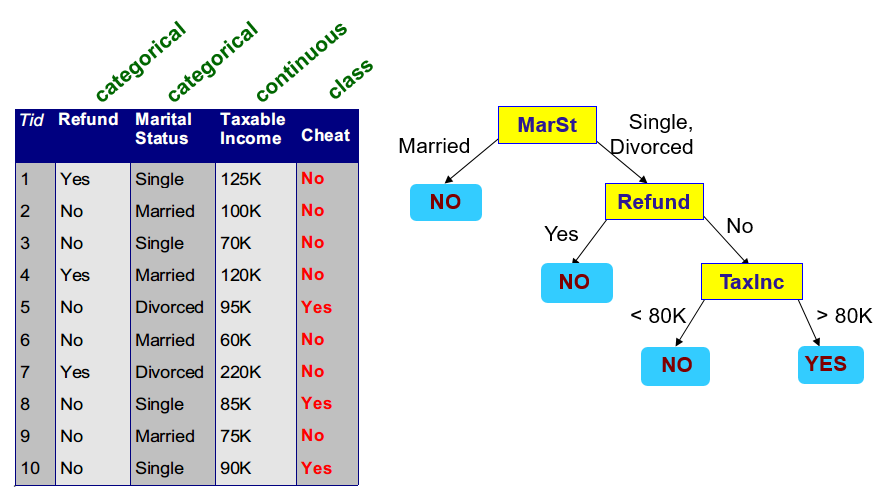
数据集给出了某个信用评价机构对用户是否欺骗的调查,其中涉及还贷情况、婚姻情况、税后收入等,其中税后收入为连续变量,其它为离散变量。根据这些数据集进行训练,可得右侧的决策树。
建立方法
根据上图可以发现,决策树的所有非叶节点相当于判断属性。如图中的决策树首先判断用户的婚姻状况,若用户已婚,则判断其不会进行欺骗行为,否则进行下一步,判断用户是否能按时还贷,等等。建立决策树的过程,即为选择最佳判断属性的过程。我们希望决策树的分支节点进行划分后,各类样本尽可能属于同一类别,即使分类之后的“纯度”最大化。
ID3算法
香农的信息论告诉我们,信息熵(information entropy)可以用来描述信源的不确定度。在ID3决策树学习算法中,就使用了这个概念。设当前样本集$D$共有$n$个属性,第$k$个分类属性中,样本所占比例为$p_k$(可看作属性$k$出现的概率),则信息熵可以表示为:
$$Ent(D)=-\sum_{k=1}^{n} p_k \log_{2}p_k$$
假设某属性$s$有$V$个可能的取值,则针对属性$s$对样本进行分类时,会产生$V$个分支节点,其中第$v$个分支表示样本集$D$中所有取值为$s^v$的样本,记作$D^v$。根据上式可以计算出$D^v$的信息熵$Ent(D^v)$。再根据不同分支点所含有的样本数量不同,对分支节点加权$\frac{|D^v|}{|D|}$,于是可得针对属性$s$对样本集$D$进行分类的信息增益(information gain):
$$Gain(D, s)=Ent(D)-\sum_{v=1}^{V} \frac{|D^v|}{|D|} Ent(D^v)$$
信息增益越大,则说明分类后的信息量越大,划分后各类别的“纯度”越大。因此可以使用信息增益作为确定最佳判断属性的依据。
C4.5算法
ID3算法采用的信息增益看上去十分完美,但其中也存在一个问题。我们再来考虑文章开始介绍的信用评价例子。若使用ID3算法对其构建决策树,则针对用户的税后收入进行分类,各类别的纯度最大。这是因为,此时ID3算法将10个样本数据划分为10类,得到的是一个深度浅、庞大而不够客观的决策树。ID3算法天然地偏向分支多的属性,而这往往不是我们想要的。C4.5算法针对这个问题,提出了信息增益率的概念。
信息增益率是用前面的信息增益$Gain(D, s)$和分裂度$Split(D, s)$来共同定义的。其中分裂度用来衡量属性分裂数据的广度和均匀,且有
$$Split(D, s)=-\sum_v \frac{|D^v|}{|D|} \log_{2} \frac{|D^v|}{|D|}$$
信息增益率为:
$$GainRadio(D, s)=\frac{Gain(D, s)}{Split(D, s)}$$
信息增益率实际上对增益进行了归一化,这样就避免了指标偏向分支多的属性的倾向。同理,增益率也可以用来克服连续值属性倾向。
纯度计算方法
其它计算纯度的方法还有:
Gini系数。假设某属性$s$有$0,1,\ldots v$共$V$个可能的取值,则有$Gini(v)=1-\sum_v [p(\frac{v}{V})]^2$。反映了随机抽取两个样本,其类别标记不一样的概率。Gini系数越小,则纯度越高。在CART算法中应用。
错误率。假设某属性$s$有$0,1,\ldots v$共$V$个可能的取值,则有$Error(v)=1-max_v p(\frac{v}{V})$。错误率越小,则纯度越高。
剪枝处理
训练出来的决策树,往往会存在过度拟合现象:决策树过于针对训练的数据,专门针对训练集创建出来的分支,其熵值可能会比真实情况有所降低。因此需要对决策树进行剪枝。
剪枝包括预先剪枝和后剪枝两种。
预先剪枝是在树的生长过程中设定一个指标,当达到该指标时就停止生长,这样做容易产生“视界局限”,一旦停止分支,使得节点N成为叶节点,就断绝了其后继节点进行“好”的分支操作的任何可能性。
后剪枝中树首先要充分生长,直到叶节点都有最小的不纯度值为止,因而可以克服“视界局限”。然后对所有相邻的成对叶节点考虑是否消去它们,如果消去能引起令人满意的不纯度增长,那么执行消去,并令它们的公共父节点成为新的叶节点。
随机森林
随机森林,就是通过集成学习的思想将多棵决策树树集成的一种算法,它的基本单元是决策树,本质是属于机器学习的分支-集成学习方法。
Bagging
随机森林是Bagging的一个扩展变体,这里首先介绍一下Bagging方法。
Bagging(Bootstrap AGGregatING)是并行式集成学习方法最著名的代表。给定包含$m$个样本的数据集,我们先随机取出一个样本放入采样集中,再把该样本放回初始数据集,使得下次采样时该样本仍有可能被选中,这样,经过$m$次随机采样操作,我们得到含$m$个样本的采样集,初始训练集中有的样本在采样集里多次出现,有的则从未出现。
样本在$m$次采样中始终不被采到的概率为$(1-\frac{1}{m})^m$,取极限有:
$${\lim_{m \to +\infty}(1-\frac{1}{m})^m}=e \approx 0.368$$
由上式可知,初始训练集中约有63.2%的样本出现在采样集中。照这样,我们可采样出$T$个含$m$个训练样本的采样集,然后基于每个采样集训练出一个基学习器,再将这些基学习器进行结合。这就是Bagging的基本流程。
进行分类任务时,Bagging通常对各基学习器的结果使用简单投票法,当票数相同时,可以随机选择一个,也可以进一步考察学习器投票的置信度来确定最终分类结果。
随机森林简介
一个随机森林由N棵决策树组成,每棵决策树都是一个基学习器,那么对于一个输入样本,N棵树会有N个分类结果。而随机森林集成了所有的分类投票结果,将投票次数最多的类别指定为最终的输出,这就是一种最简单的Bagging思想。
与Bagging不同的是,随机森林在决策树的训练过程中,引入了随机属性选择:对每个节点,先从该节点的属性集合中随机选择一个包含$k$个属性的子集,然后再从子集中选择一个最优属性进行划分。这里若$k=d$,则与传统决策树构建思路相同,一般推荐取$k=\log_2 d$。
随机森林简单、容易实现、计算开销小。令人惊奇的是,它在很多现实任务中展现出强大的性能,被誉为“代表集成学习技术水平的方法”。可以看出,随机森林对Bagging只做了小改动,但是与Bagging中基学习器的“多样性”仅通过样本扰动(通过对初始训练集采样)而来不同,随机森林中基学习器的多样性不仅来自样本扰动,还来自属性扰动,这就使得最终集成的泛化性能可通过个体学习器之间差异度的增加而进一步提升。
参考文献
- 机器学习. 周志华. 北京: 清华大学出版社
- 决策树 - 维基百科.
- 数据挖掘十大算法详解.