背包问题概述
背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。通过暴力搜索,枚举所有可能性,可以找出最优解。但这里我们主要讨论动态规划(Dynamic programming,DP)解法:背包问题作为NP完全问题,暂时不存在多项式时间算法,动态规划属于背包问题求解最优解的可行方法之一。
0-1背包问题
问题描述
在0-1背包问题中,给定每种物品仅有一个,对于每个物品,都有“选择”与“不选择”两个状态。
下面给出一个具体的问题:有编号分别为$a,b,c,d,e$的五件物品,它们的重量分别是$2,2,6,5,4$,它们的价值分别是$6,3,5,4,6$,现在给你个承重为10的背包,如何让背包里装入的物品具有最大的价值总和?
解决方法
在动态规划中,状态转移方程是一个重要概念,它用来确定如何从一个状态转移到下一个状态。对上面的例子,状态转移方程可以表示为:
$$F[i, v] = max{F [i − 1, v], F [i − 1, v − C_i ] + W_i }$$
这个方程非常重要,基本上所有跟背包相关的问题的方程都是由它衍生出来的,所以有必要将它详细解释一下:“将前$i$件物品放入容量为$v$的背包中”这个子问题,若只考虑第$i$件物品的策略(放或不放),那么就可以转化为一个只和前$i − 1$件物品相关的问题:如果不放第$i$件物品,那么问题就转化为“前$i − 1$件物品放入容量为$v$的背包中”,价值为$F[i − 1, v]$;如果放第$i$件物品,那么问题就转化为“前$i − 1$件物品放入剩下的容量为$v − C_i$的背包中”,此时能获得的最大价值就是$F[i − 1, v − C_i]$再加上通过放入第$i$件物品获得的价值$W_i$。
我们用下面的表格来描述这个问题。为了叙述方便,用$e2$单元格表示$e$行2列的单元格,这个单元格的意义是用来表示只有物品$e$时,有个承重为2的背包,那么这个背包的最大价值是0,因为$$物品的重量是4,背包装不了。对于d2单元格,表示只有物品$e,d$时,承重为2的背包,所能装入的最大价值,仍然是0,因为物品$e,d$都不是这个背包能装的。同理,$c2=0,b2=3,a2=6$。
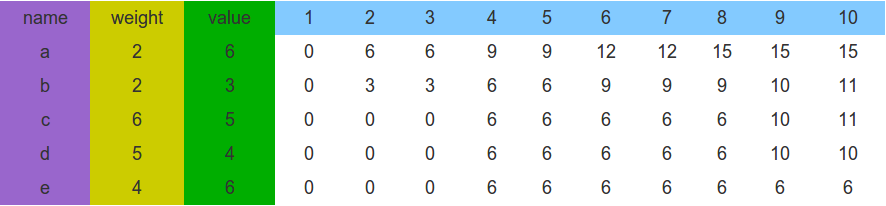
对于承重为8的背包,$a8=15$,是怎么得出的呢?根据0-1背包的状态转换方程,需要考察两个值,一个是$F[i-1,v]$,对于这个例子来说就是$b8$的值9,另一个是$F[i-1,v−C_i]+W_i$;在这里,$F[i-1,v]$表示我有一个承重为8的背包,当只有物品$b,c,d,e$四件可选时,这个背包能装入的最大价值。$F[i-1,v−C_i]$表示我有一个承重为6的背包(等于当前背包承重减去物品$a$的重量),当只有物品$b,c,d,e$四件可选时,这个背包能装入的最大价值。$F[i - 1, v − C_i]$就是指单元格$b6$,值为9,$P_i$指的是a物品的价值,即6。由于$F[i-1, v − C_i]+W_i = 9 + 6 = 15$大于$F[i-1,v]$,所以物品a应该放入承重为8的背包。
空间优化
对于上面的算法,时间复杂度应该是不能再进行优化了,但是我们还可以对空间进行优化。注意到状态转移方程中$F[i, v]$的值只与$F[i-1, x], x=1,2,3,\ldots, v$有关,因此可以缩减成一维数组,状态转移方程转换为:
$$F[v]=max(F[v], F[v - c[i]] + W_i)$$
其它背包问题
完全背包问题
与0-1背包问题的区别是:在0-1背包问题中,每个物品仅有一件;在完全背包问题中,每个物品有无限件。
完全背包问题有一个很简单有效的优化:若两件物品$i,j$满足$C_i \leq C_j$且$W_i \geq W_j$,则可以将物品$j$去掉,因为物品$j$占空间大、价值低,不予考虑至少不会吃亏。
我们可以将完全背包问题转化为0-1背包问题求解。最简单的想法是,考虑到第$i$件物品最多选$\lfloor V /C_i \rfloor$件,于是可以把第$i$种物品转化为$\lfloor V /C_i \rfloor$件费用及价值均不变的物品,然后求解这个0-1背包问题。例如背包大小为20,某物品$i$占体积费用$C_i=3$,则该物品最多装6个,这时可以假设有6个同样的物品$i$(而不是无限个)。
更为高效的做法是利用二进制的思想:把第$i$件物品拆成费用为$C_i2^k$、价值为$W_i2^k$的若干件物品,其中$k$是使得$C_i2^k\leq V$的自然数。参考上例,我们可以把第$i$件物品拆成费用为$3$、价值为$W_i$,费用为$6$、价值为$2W_i$与费用为$12$、价值为$4W_i$的3件物品。这里相当于把十进制数字6用3位二进制数字表示。
多重背包问题
与完全背包问题的区别是:在完全背包问题中,每个物品有无限件;在多重背包问题中,每个物品有$M_i$件。
一种容易想到的方法是,与完全背包问题同理,将多重背包问题转化为0-1背包问题求解。同时,我们仍然可以利用二进制的思想,但此时要注意物品是有限的,放入背包的物品数量不能超过其件数$M_i$。解决方法是:将第$i$种物品分成若干件0-1背包中的物品,其中每件物品有一个系数。这件物品的费用和价值均是原来的费用和价值乘以这个系数。系数的范围是:$1,2,2^2, \ldots, 2^{k-1},M_i-2^k+1$,$k$是满足$M_i-2^k+1 > 0$的最大整数。例如,如果$M_i=14$,则$k=3$,这个最多取14件的物品应被分成系数为$1,2,4,7$的四件物品。
混合背包问题
混合背包问题相当于上面提到所有背包问题的混合:有的物品仅有1件,有的物品有无限件,有的物品有$M_i$件(有限件)。与上面的理论相同,分类进行转化即可,不再赘述。
参考文献
- 背包问题九讲. 崔添翼.
- 背包问题 - 维基百科