利用Tensorflow构建深度学习模型

发表于 更新于

本文主要介绍如何使用Tensorflow框架作为深度学习的工具，构建模型并求解问题。

Tensorflow概述

简介

TensorFlow是一个开源软件库，用于各种感知和语言理解任务的机器学习。TensorFlow可以运行在多个CPU和GPU。TensorFlow可用于64位Linux、macOS和Windows，以及移动计算平台，包括Android和iOS。

下面给出一张示意图，以描述Tensorflow的工作流程。

Tensorflow数据流图

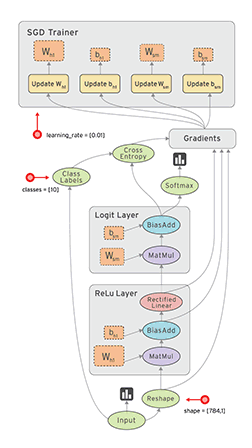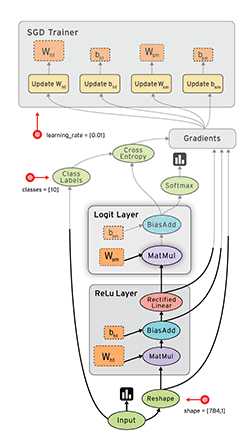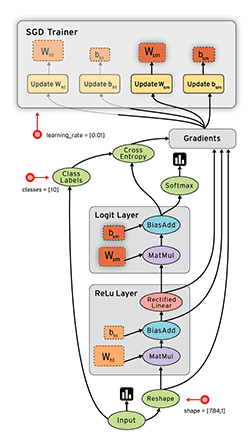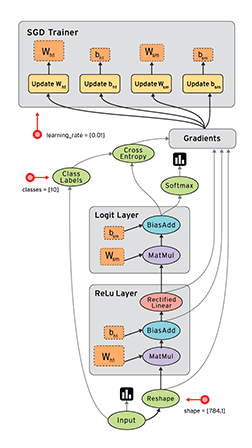
数据流图用“节点”（nodes）和“线”(edges)的有向图来描述数学计算。“节点” 一般用来表示施加的数学操作，但也可以表示数据输入（feed in）的起点，或输出（push out）的终点，或者是读取/写入持久变量（persistent variable）的终点。“线”表示“节点”之间的输入/输出关系。这些数据“线”可以输运“size可动态调整”的多维数据数组，即“张量”（tensor）。张量从图中流过的直观图像是这个工具取名为“Tensorflow”的原因。一旦输入端的所有张量准备好，节点将被分配到各种计算设备完成异步并行地执行运算。

一个简单示例

假设我们需要拟合一个平面：$y=0.1x_1 + 0.2x_2 + 0.3$。神经网络的表达式为：$y=W_1x_1 + W_2x_2 + b$，示意分别如图。

平面与神经网络模型示意图

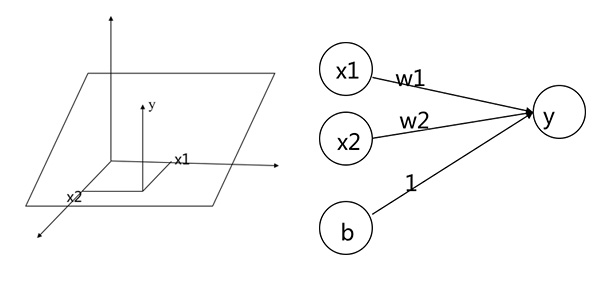
下面针对程序代码说明如何使用Tensorflow求解这个问题。首先构建模型：

1
2
3
4
# 构建模型
b = tf.Variable(tf.zeros([1]))
W = tf.Variable(tf.random_uniform([1, 2], -1.0, 1.0))
y = tf.matmul(W, x_data) + b

这里定义了b、W、y三个参数，b是尺寸为1的张量，W是均匀分布的随机数，取值为[-1.0, 1.0]，尺寸为[1, 2]。y是W与x作矩阵乘法后再加b。

1
2
# 构造误差函数
loss = tf.reduce_mean(tf.square(y - y_data))

这里定义了误差函数，y是预测值，y.data是实际值。

1
2
3
# 构造优化器
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)

使用梯度下降法进行求解，目的是最小化误差。

1
2
3
4
5
6
7
8
9
10
# 初始化变量
init = tf.initialize_all_variables()

# 启动会话
sess = tf.Session()
sess.run(init)

# 训练
for step in xrange(0, 201):
    sess.run(train)

之后就是套路性质的代码了，初始化变量、启动会话、开始训练。会话（Session）是Tensorflow为了控制和输出文件的执行的语句。

利用多个GPU加速计算

Tensorflow可以在CPU与GPU间无缝切换。由于GPU的特性，它非常适合机器学习的计算。其工作模型如图。

多GPU板卡示意图

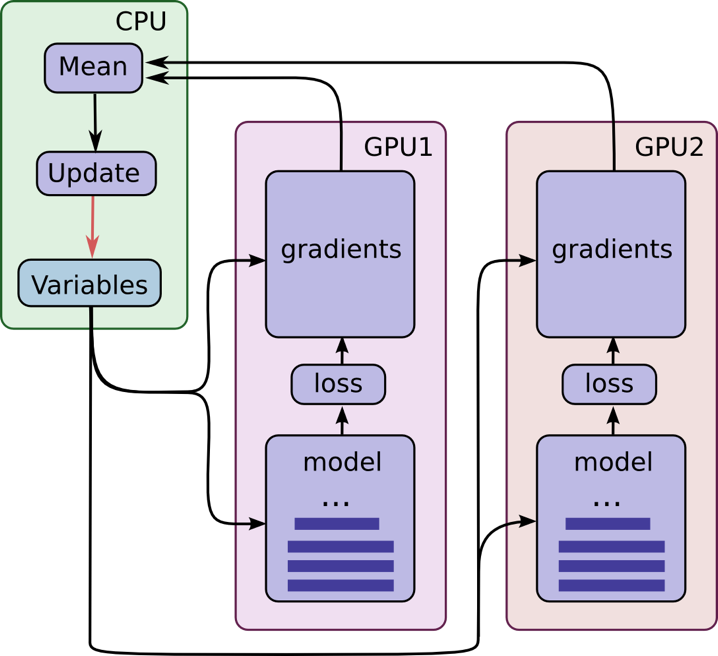
其机制可概括为：在每个GPU上放置单独的模型副本，等所有GPU处理完一批数据后再同步更新模型的参数。这一机制要求所有GPU能够共享模型参数，但在GPU之间传输数据非常慢，因此在CPU上存储和更新所有模型的参数。这样一来，GPU在处理一批新的数据之前会更新一遍的参数。

图中所有的GPU是同步运行的。所有GPU中的梯度会累积并求平均值。模型参数会利用所有模型副本梯度的均值来更新。

MNIST手写数字识别

当我们开始学习编程的时候，第一件事往往是学习打印”Hello World”。就好比编程入门有Hello World，机器学习入门有MNIST。MNIST是一个入门级的计算机视觉数据集，它包含各种手写数字图片及其标签（告诉我们它是哪个数字），提供了60000行的训练数据集和10000行的测试数据集。下面我们主要利用它来进一步学习。

图像的数据结构

在计算机中，图像实际上被看作一个矩阵，如图。

图像数据结构示意图

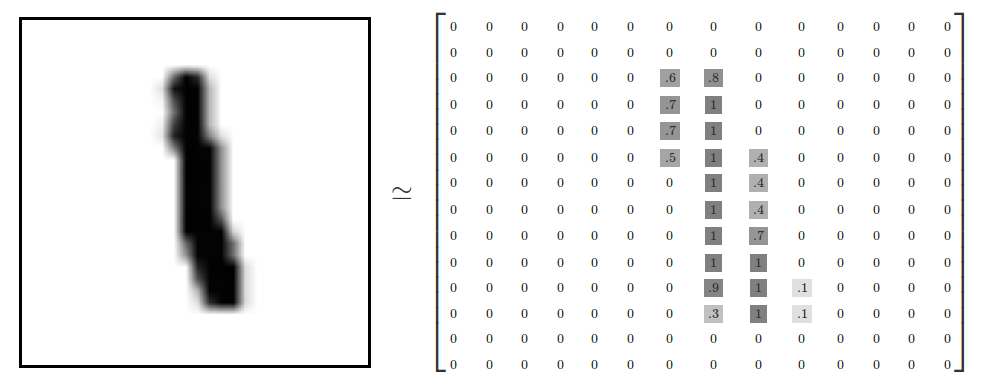
这个矩阵可表示为长×宽×色道数。因为示意图是黑白单色，所以只有一个维度。彩色图片有多个维度。

MNIST数据集的长和宽均为28个像素。为便于分析，我们使标签数据是“one-hot vectors”。 一个one-hot向量除了某一位的数字是1以外，其余各维度数字都是0。所以，数字n将表示成一个只有在第n维度（从0开始）数字为1的10维向量。比如，标签0将表示成[1,0,0,0,0,0,0,0,0,0,0]。

softmax回归

在softmax回归中，我们解决的是多分类问题，类标$y$可以取$k$个不同的值。因此，对于训练集${ (x^{(1)}, y^{(1)}), \ldots, (x^{(m)}, y^{(m)}) }$，我们有$y^{(i)} \in {1, 2, \ldots, k}$。（注意此处的类别下标从1开始，而不是0）。例如，在MNIST数字识别任务中，我们有$k=10$个不同的类别。

对于给定的测试输入$x$，我们想用假设函数针对每一个类别j估算出概率值$p(y=j丨x)$。也就是说，我们想估计$x$的每一种分类结果出现的概率。因此，我们的假设函数将要输出一个$k$维的向量（向量元素的和为1）来表示这$k$估计的概率值。 具体地说，我们的假设函数$h_{\theta}(x)$形式如下：

$$
h_\theta(x^{(i)}) =
\begin{bmatrix}
p(y^{(i)} = 1 | x^{(i)}; \theta) \
p(y^{(i)} = 2 | x^{(i)}; \theta) \
\vdots \
p(y^{(i)} = k | x^{(i)}; \theta)
\end{bmatrix}

\frac{1}{ \sum_{j=1}^{k}{e^{ \theta_j^T x^{(i)} }} }
\begin{bmatrix}
e^{ \theta_1^T x^{(i)} } \
e^{ \theta_2^T x^{(i)} } \
\vdots \
e^{ \theta_k^T x^{(i)} } \
\end{bmatrix}
$$

其中$\theta_1, \theta_2, \ldots, \theta_k \in \Re^{n+1}$是模型的参数。请注意$\frac{1}{ \sum_{j=1}^{k}{e^{ \theta_j^T x^{(i)} }} }$这一项对概率分布进行归一化，使得所有概率之和为1。

为了方便起见，我们同样使用符号$\theta$来表示全部的模型参数。在实现Softmax回归时，将$\theta$用一个$k \times(n+1)$的矩阵来表示会很方便，该矩阵是将$\theta_1, \theta_2, \ldots, \theta_k$按行罗列起来得到的，如下所示：

$$
\theta = \begin{bmatrix}
-\theta_1^T-\
-\theta_2^T- \
\vdots \
-\theta_k^T- \
\end{bmatrix}
$$

为表示方便，引入示性函数的概念。$1 { \cdot }$是示性函数，其取值规则为：$1 { True }=1$，$1 { False }=0$，则代价函数可表示为：

$$
J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left{y^{(i)} = j\right} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }}\right]
$$

注意在Softmax回归中将$x$分类为类别$j$的概率为：

$$
p(y^{(i)} = j | x^{(i)} ; \theta) = \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)}} }
$$

对于$J(\theta)$的最小化问题，目前还没有闭式解法。因此，我们使用迭代的优化算法（例如梯度下降法）。经过求导，我们得到梯度公式如下：

$$
\nabla_{\theta_j} J(\theta) = - \frac{1}{m} \sum_{i=1}^{m}{ \left[ x^{(i)} \left( 1{ y^{(i)} = j} - p(y^{(i)} = j | x^{(i)}; \theta) \right) \right] }
$$

$\nabla_{\theta_j} J(\theta)$本身是一个向量，它的第$l$个元素$\frac{\partial J(\theta)}{\partial \theta_{jl}}$是$J(\theta)$对$\theta_j$的第$l$个分量的偏导数。有了上面的偏导数公式以后，我们就可以将它代入到梯度下降法等算法中，来最小化$J(\theta)$。

示例代码

1
2
3
# 占位符
x = tf.placeholder("float",shape=[None, 784])
y_ = tf.placeholder("float",shape=[None, 10])

x不是一个特定的值，而是一个占位符placeholder，我们在TensorFlow运行计算时输入这个值。这里的None表示此张量的第一个维度可以是任何长度的，第二个值784即为28×28（长×宽）。y是预测的概率分布，10即为one-hot向量维度。

1
2
3
W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))
y = tf.nn.softmax(tf.matmul(x,W) + b)

用全为零的张量来初始化W和b。因为我们要学习W和b的值，它们的初值可以随意设置。W的维度是[784，10]，因为我们想要用784维的图片向量乘以它以得到一个10维的证据值向量，每一位对应不同数字类。b的形状是[10]，所以我们可以直接把它加到输出上面。tf.matmul(​​x，W)表示x乘以W，对应之前等式里面的$Wx$，然后再加上b，最后把结果输入到tf.nn.softmax函数里面。

参考文献