基于频率子图分析的Android恶意软件家族分类与典型样例选取

发表于 2019-01-02 更新于 2023-03-22

本文介绍2018年IEEE Transactions on Information Forensics and Security的一篇文章，题目是《Android Malware Familial Classification and Representative Sample Selection via Frequent Subgraph Analysis》，DOI信息在这里。

在阅读完最近一篇博文提及的文章后，我发现其方法非常适合用于恶意软件家族分类，于是进行了调研，结果发现了同一作者新发表的文章，主要研究内容即为家族分类。本文即将介绍这篇论文。

这条文章通过建立频率子图（frequent subgraph），表示属于同一家族恶意软件样本的一般行为。基于以上方法，作者提出并开发了FalDroid，一个依照频率子图自动对Android恶意软件进行分类并选择典型样本的新颖系统。

摘要

Android恶意软件数量的快速增长为反恶意软件系统带来了巨大的挑战，因为恶意软件样本数量的陡升超过了恶意软件分析系统的处理能力。将恶意软件样本划分为不同家族，利用同一家族样本所具有的共性特征进行恶意软件检测，是加速恶意软件分析的一种前景较好的方法。此外，在每个家族中选择具有典型性的恶意软件样本可以大大减少需要分析的恶意软件的数量。然而，由于以下原因，现有的分类方法存在局限性。首先，恶意软件的合法部分可能会误导分类算法，因为大多数Android恶意软件是通过将恶意组件插入流行APP构建的。第二，Android恶意软件的变种可以通过使用变形攻击（transformation attack）来逃避检测。在本文中，作者提出一种新颖方法，通过建立频率子图，表示同一家族恶意软件样本的一般行为。此外，作者提出并开发了FalDroid，一个依照频率子图自动对Android恶意软件进行分类并选择典型样本的新颖系统。通过对36个家族、8407个样本的评估，FalDroid能够达到94.2%的准确率，平均每个APP耗时4.6秒。FalDroid还可以通过选择在所有样本中占8.5%-22%的、表现出最常见恶意行为的典型样本，显著降低恶意软件调查的成本。

简介

在2016年的第三季度，Android作为最受欢迎的移动操作系统，占有智能手机市场86.8%的份额。同时，它也成为97%移动平台恶意软件的主要目标。一份近来的安全报告显示，在2016年的第三季度，平均每天捕获到38000个新的移动平台恶意软件样本。对每个恶意软件样本的分析需要大量时间。因此，恶意软件样本数量的陡升超过了恶意软件分析系统。

大多数新的恶意软件样本是已知恶意软件的多态变种。因此，为了加速恶意软件的分析，我们可以将恶意软件样本分为不同的家族，然后从每个家族中选择有典型性的样本。然而，Android恶意软件的家族分类具有挑战性，原因有二。

第一，一些Android恶意软件是对受欢迎APP的重新打包，准确分离它们的可疑组件与合法部分并非易事。文献指出，86%的Android恶意软件是通过在良性APP中插入恶意组件重新打包生成的。这些被插入的恶意组件藏在受欢迎APP的功能中，通常只占一小部分。现有特征，如系统调用与敏感路径，很难区分恶意软件的合法部分和恶意组件。

第二，由于来自同一家族的Android恶意软件具有多样性，尽管实现方法可能不同，但它们的恶意行为是相同的。因此，这样的恶意软件可以很容易地逃避现有的、寻找特定模式的分类解决方案。下图展示了同一功能（即获取设备ID、电话号码与语音信箱号码）的不同实现方式。两个恶意软件样本来自同一家族geinimi。这些类似bot的恶意软件样本窃取个人信息并将其发送到远程服务器。在这两个实现中可以观察到三个主要的区别(红色突出显示)。首先，类名的结构不同。第二，两个函数的参数不同。一个使用service作为参数，另一个使用类rally/e的对象作为参数。第三，前一个函数比第二个包含两个更多的程序语句，其中还包括一个调用。

来自geinimi家族的两个恶意软件样本对同一功能的不同实现

为解决以上问题，文章作者利用以下两个观察结果，提出了一个新颖的方法：

Android恶意软件为进行恶意行为，通常需要引用操作敏感数据的敏感API。例如，上图中的恶意软件样例使用了*getLine1Number()*以获得用户的手机号码。
恶意软件及其在同一家族中的变体调用敏感API的模式相似，即使它们的代码可能经过混淆。上图中，有三个常使用的敏感API（*getDeviceID()、getLine1Number()与getVoiceMailNumber()*，已使用蓝色标记）在两个不同样本的方法（method）中均有存在。这三个敏感API调用是在这两个方法中依次调用的，从而说明在同一家族的不同样本中，敏感API调用存在类似的模式。

通过使用这两个观察结果，作者首先将程序语义提炼为函数调用图（function call graph，FCG），使用类似TF-IDF的方法为每个敏感API调用赋予不同的权重。之后，作者提出两个关键技术以解决上述问题：

基于聚类的方法，提取每个家族的共有恶意行为，并定重新打包生成APP的恶意部分与良性部分的错误划分。因此可以减少恶意软件良性部分的副作用。
对同一功能的不同实现方法，提出基于加权敏感API调用图的匹配方法，以计算由社群检测算法（community detection algorithm）生成的图之间的相似度。社群检测算法用于判断一个图的节点是否具有社群结构，是否可以方便地将图中的节点分组为节点集，使每一组节点内部连接紧密。
这些方法可以检测同一家族的恶意行为，同时可以容忍实现上的细微差异，比如函数重命名和垃圾代码插入。敏感API调用只占整个Android API调用的一小部分，现有的典型混淆技术无法轻易混淆它们，而用户定义的函数名称通常被混淆为a、b或c。

为表示恶意软件样本在同一家族中共有的常见恶意行为，作者基于两个关键技术，构造了频率子图（frequent subgraph, fregraph），即从生成的FCG中提取的基于图形的新特征。此外，作者提出并开发了FalDroid系统，它是一个自动系统，用于对Android恶意软件进行分类，并根据fregraph选择具有代表性的样本。作者将FalDroid应用于36个家族的8407个恶意软件，发现它具有令人印象深刻的家族分类性能。此外，它可以有效减少工作量，加速恶意软件分析。

FalDroid方法

下图展示了FalDroid的总体结构，它由三个主要阶段组成。

FalDroid总体结构概览

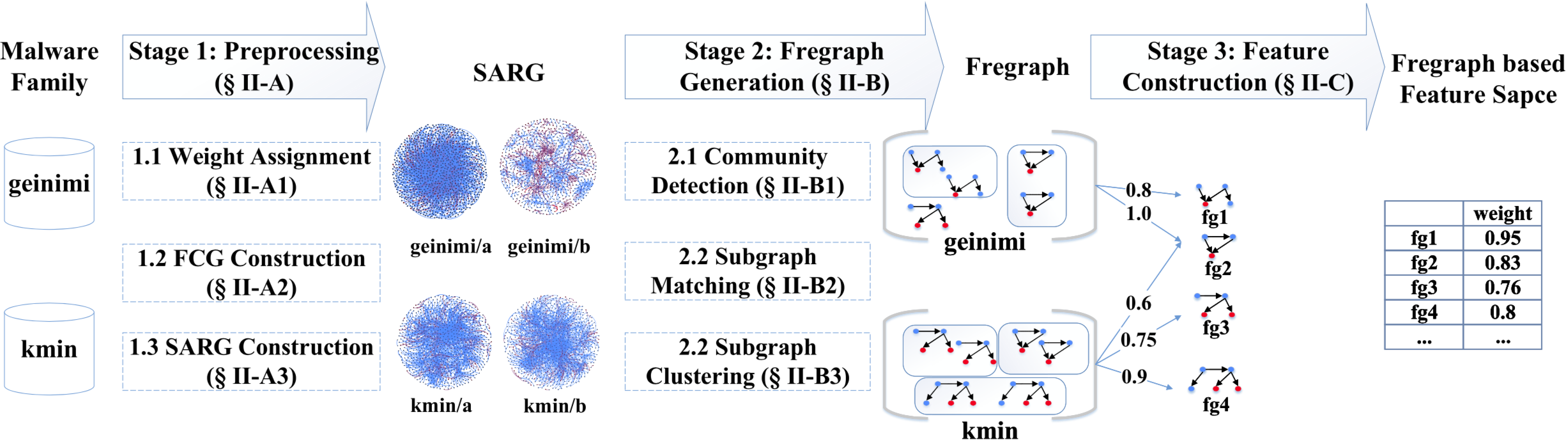
预处理阶段为每个APP构建基本行为模型，它包含三个过程。首先，考虑到敏感API调用的重要性在不同家族中是不同的，使用类似TF-IDF的方法，为每个敏感API赋予不同权重，以区分它们的重要性。第二，为描述一个APP的程序语义，构造一个FCG，以其反汇编得到的代码为基础来表示该APP。第三，考虑到FCG通常包含上千个节点，直接分析非常耗时，因此先将FCG简化为敏感API调用相关图（sensitive API call related graph，SARG，定义1），只保留敏感API节点与它们的父节点。所以，既维护了APP的恶意行为信息，又降低了图模型的复杂性。

在fregraph生成阶段，生成fregraph以表示同一家族的恶意软件共有的恶意行为。为方便定位不同恶意软件的共有功能，降低图相似度计算的复杂性，使用社群检测算法将SARG初步划分为一组子图。特别地，带有敏感API调用节点的子图被命名为敏感子图（定义2）。利用子图匹配和聚类技术，将一个家族中大多数样本使用的敏感子图定义为特定家族的fregraph（定义3）。

在特征建立阶段，为每个APP建立一个特征向量。在此基础上，利用已知的机器学习算法可以完成家族分类任务。为此，将已知的所有家族的fregraph嵌入到一个特征空间中，并对每个fregraph进行加权评分，以表明其对恶意软件家族分析的重要性。

预处理

Android APP通常使用Java编写，被编译为Dalvik代码，保存在classes.dex文件中。编译后的代码与需要的资源文件被打包进APK文件中。可以使用反汇编工具（如apktool）从APK中获取Dalvik代码。

Android恶意软件通常调用操作敏感数据的敏感API，以进行恶意活动。通过调研文献，得到了共计26322个敏感API。

敏感API调用的权重分配

为区分不同敏感API调用的重要性，对不同家族的不同敏感API调用进行了权重分配。文章为家族$f$的每个API调用$s$定义了三个度量标准，以描述其在不同家族中的使用情况。

$num(s, f)$：在家族$f$中，调用敏感API$s$的样本数量。
$per(s, f)$：在家族$f$中，调用敏感API$s$的样本占比。$per(s, f) = \frac{num(s, f)}{falNum(f)}$，其中，$falNum(f)$表示家族$f$中的样本数量。
$w(s, f)$：在家族$f$中，敏感API调用$s$的权重。

此外，使用$allNum$表示收集的全部样本数量，使用$totalNum(s)$表示在所有家族中，调用敏感API$s$的样本数量。$totalNum(s)= \sum_{f_j \in F} num(s, f_j)$，其中$F={ f_j | 1 \leq j \leq m }$，$m$表示家族的数量。

下表展示了6个敏感API调用的相关数据，其中包括$totalNum$、$num$、$per$与$w$。可以观察到，同一家族中不同敏感API调用的使用是不同的。例如，sendTextMessage()在geinimi家族的所有105个样本中均被使用，但*divideMessage()仅被6个样本使用。此外，一些敏感API调用（如getDeviceId()*）被多数恶意软件样本使用。

6个敏感API调用的相关数据

以上两个观察结果说明，某一家族的某个敏感API调用的权重，应该与它的$per$正相关，与它的$totalNum$负相关。通过借用TF-IDF的思路，文章提出一种类似TF-IDF的方法，使用TF度量家族$f$中敏感API调用$s$的频率，使用IDF度量出现在所有恶意软件样本中的$s$的反频率。之后，在家族$f$中，敏感API调用$s$的权重可以表示为：
$$
w(s, f) = per(s, f) * \log \frac{allNum}{totalNum(s)}
$$

上表同时给出了敏感API调用的权重。其中，在$geinimi$家族中的*sendTextMessage()的权重是0.567，相比divideMessage()的权重仅为0.080，这是因为sendTextMessage()的$per$明显高于divideMessage()。此外，getDeviceId()*被三个家族的样本使用，因此对于恶意软件分类而言，它不太重要。它的权重仅为0.083，明显低于其它敏感API调用的权重。直觉来看，结果表明，我们的方法的权重分配可以有效地衡量敏感API调用对一个家族的重要性。

FCG的建立

对APK文件使用apktool之后，可以得到它的Dalvik代码。然后，通过识别调用语句（如invoke-direct）从Dalvik代码中提取调用函数和被调用函数。之后，将这些调用函数和被调用函数作为节点添加到图中，如果两个节点存在调用关系，则在它们之间添加一条边。这样，可以将APP的程序语义抽象为FCG，FCG包含了描述APP行为所需的结构信息。FCG用有向图$G=(V,E)$表示。

SARG的建立

FCG中包含上千个节点。分析整个FCG既难以见效（恶意部分隐藏在良性部分中），又缺乏效率（节点和边过多）。因此，作者排除了没有路径到敏感API调用节点的节点，以减少图分析的复杂性，这样FCG $G$被简化为SARG $G’$。将表示敏感API调用的节点指定为敏感API调用节点（sensitive API call node）。

定义1 （SARG）： SARG是FCG的诱导子图，其中每个节点至少有一个指向敏感API调用节点的直接路径，或者节点本身是一个敏感API调用节点。

SARG $G’=(V’, E’)$可以由下面两个公式得出，其中$V_s \subseteq V$是APP使用的敏感API调用的集合，函数$dis(v_j, v_i)$返回从节点$v_j$到节点$v_i$的最短路径长度。

$$
V_g = { v_j | \exists v_i \in V_s, 0 < dis(v_j, v_i) < n, v_j \in V }
$$
$$
V’ = V_s \cup V_g, E’ = (V’ \times V’) \cap E
$$

普遍看来，SARG的体积比原有的FCG减少了72%。下图展示了一个geinimi家族的恶意软件的原FCG（2000个节点）与它的SARG（450个节点），其中红色节点代表敏感API调用节点，蓝色节点代表普通节点。红色边表示被调用函数是敏感API调用节点。

原FCG与其生成的SARG

Fregraph生成

社群检测

在预处理阶段之后，通过观察同一家族生成的SARG，可以得出如下结论：同一家族的APP具有相似的子图，这些子图仅占SARG的一小部分，即使它们SARG的大部分是不同的。生成SARG的一小部分表示同一家族中恶意软件样本的常见恶意功能，而其它大部分SARG表示不同的良性功能。

下图展示了来自geinimi家族的两个不同样本的SARG，它们分别包含267与715个节点。红圈标记的子图几乎相同，说明行为相似，而其它部分则完全不同。由于图的同构问题是NP完备的，直接从SARG中识别相似子图的效率较低。因此，文章将SARG分成一组更小的子图的集合，以方便地定位不同恶意软件样本的共同功能，并降低图形相似度计算的复杂性。

两个来自geinimi家族的SARG

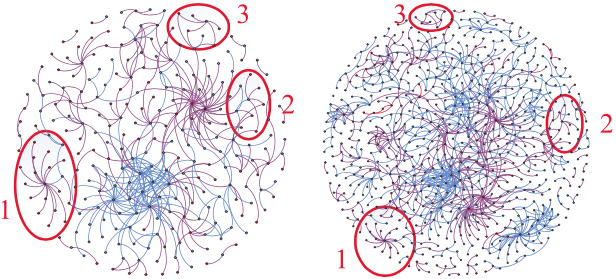
有文献指出，社群结构（community structure）是一个主要的网络特征，它指的是将顶点聚集成组，使得组内的边密度大于组间的边密度。之前的研究已经证明，FCG是具有社群结构的典型网络。一个社群结构中的软件功能具有很强的联系，常常位于同一个类或包中，以实现共同的软件功能。

为判断生成的SARG是否为具有社群结构的网络，作者采用了4个广泛使用的社群检测算法，包括infomap、fast greedy、fast partitioning与multilevel，将SARG分为若干个子图。文章使用Networkx实现算法，这是一个计算复杂网络的程序包。在实验中，作者选择infomap作为主要的社区检测算法，因为它比其它3种算法生成的子图更多、节点更少，从而有效地减少了图匹配的复杂性。

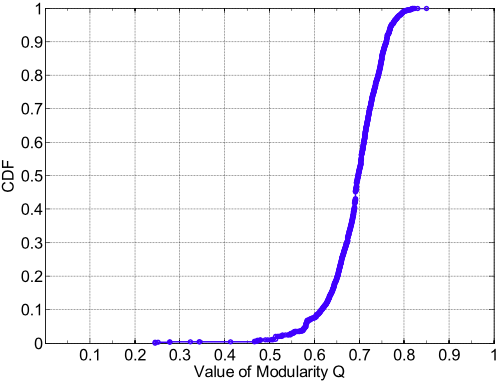
Newman与Girvan在文献中提出模块度（modularity）$Q$的概念，以量化检测到的社群结构的质量。当$Q$接近0时，表示没有找到社群结构。相反，当$Q$接近1时，表示找到了一个理想的社群结构。文章使用infomap算法评估数据集生成的SARG。下图使用模块度$Q$的累积分布函数（cumulative distribution function，CDF）图。超过90%的$Q$值在0.6到0.8之间。该范围表明生成的SARG具有显著的社群结构。

使用infomap算法时$Q$的CDF图

此外，考虑到大多数由社群检测算法划分的子图与敏感数据没有关系，它们可能对恶意软件的分类帮助不大。因此，文章定义了敏感子图。

定义2 （敏感子图）： 敏感子图是由SARG使用社群检测算法划分的子图，其中包含至少一个敏感API调用节点。来自同一个SARG的任意两个敏感子图中不存在公共节点。

来自家族$f$的敏感子图$sg$拥有权重$w(sg, f)$，以表示它对于$f$的重要性。下式定义了$w(sg, f)$，其中$V_s(sg)$是$sg$中敏感API调用节点的集合。
$$
w(sg, f) = \sum_{v_i \in V_s(sg)} w(v_i, f)
$$

子图匹配

为量化两个子图的相似度，文章提出了一种新颖的、基于加权敏感API调用的方法，能够检测同一家族内的同类恶意软件的行为，并能容忍实现上的微小差异。

来自家族$f$的两个子图$sg_1$与$sg_2$示意图

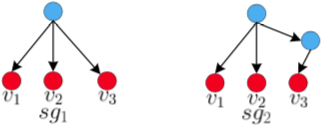
上图展示了来自家族$f$的两个子图样例$sg_1$与$sg_2$。每个子图均包含三个敏感API调用节点$v_1$、$v_2$与$v_3$。假设这三个节点使用类似TF-IDF方法得到的权重分别为0.2、0.5与0.8。为计算家族$f$中$sg_1$与$sg_2$的相似度，文章聚焦于它们敏感API调用节点之间的相似性，因为这些节点不能通过典型的混淆技术轻易更改。两个子图中相同敏感API调用节点之间的相似性在结构等价的基础上进行计算。结构等价假设指出，子图中具有相似结构角色的节点应该集中、紧密地嵌入相同的特征空间。具体来说，相似度$sim_f(sg_1,sg_2)$分以下三步计算。

步骤1 （为两个子图建立距离矩阵）： 首先，为每个子图建立距离矩阵，用于测量特定子图中不同敏感API调用节点之间的关系。$sg_k (k=1,2)$的矩阵由以下公式得出，它的大小是$t\times t, t = | V_s(sg_1)\cup V_s(sg_2) |$。下式中，在计算两个节点$v_i$到$v_j$之间的最短路径距离$dis’(v_i, v_j)$时，将图看作无向图。

$$
Matrix_k[i, j] = \left{ \begin{array}{lc}
dis’(v_i, v_j), & v_i, v_j \in V_s(sg_k)\
\infty, & otherwise
\end{array} \right.
$$

在上面的图片中展示的两个子图，其构建的距离矩阵大小是$3\times 3$，$Matrix_1[1, 3] = 2$，$Matrix_2[1, 3] = 3$，考虑到$sg_2$从$v_1$到$v_3$的路径比$sg_1$多了一个额外的节点。

步骤2 （计算敏感节点的相似度）： 为形式化敏感API调用节点在子图结构中的角色，文章通过下式将其嵌入一个$t$维的向量。每个维度的值基于当前敏感API调用节点与其它敏感API调用节点之间的最短距离计算得出。之后使用标准余弦度量$sg_1$与$sg_2$中同一敏感API节点的相似性$ns(v_i)$。

$$
\overrightarrow{vec(v_i, sg_k)} = \langle \frac{1}{Matrix_k[i, 1]}, \ldots , \frac{1}{Matrix_k[i, t]} \rangle
$$

$$
ns(v_i) = cos(\overrightarrow{vec(v_i, sg_1)}, \overrightarrow{vec(v_i, sg_2)})
$$

在上面的图片中展示的两个子图，其中$v_1$根据步骤2计算的向量是$\overrightarrow{vec(v_1, sg_1)} = \langle 0, \frac{1}{2}, \frac{1}{2} \rangle$与$\overrightarrow{vec(v_1, sg_2)} = \langle 0, \frac{1}{2}, \frac{1}{3} \rangle$。同样可以计算出$ns(v_2)=0.98$，$ns(v_3)=1.0$。

步骤3 （计算子图的相似度）： 考虑到每个敏感API调用节点都被赋予一个权重，以表示它对于特定家族$f$的重要性，文章使用两个子图相交节点间余弦距离的归一化加权和计算$sim_f(sg_1, sg_2)$。

$$
sim_f(sg_1, sg_2) = \frac{\sum_{v_i\in V_s(sg_1)\cap V_s(sg_2)} (w(v_i, f) * ns(v_i))}{\sum_{v_i\in V_s(sg_1)\cup V_s(sg_2)} w(v_i, f)}
$$

由此，上面的图片中展示的两个子图的相似度是$sim_f(sg_1, sg_2) = \frac{0.98 \times 0.2 + 0.98 \times 0.5 + 1.0 \times 0.8}{0.2 + 0.5 + 0.8} = 0.99$。最大值1表示这两个子图表现出完全相同的行为，而最小值0表示这两个子图表现出完全不同的行为。实例表明，文章的子图相似度计算方法能够很好地容忍实现上的微小差异。

子图聚类

利用有效的图匹配方法，在不需要先验知识的情况下，基于子图聚类生成fregraph。

子图聚类算法

上面的算法列出了子图聚类的过程。算法的输入是家族$f$敏感子图的集合与阈值$\epsilon$，输出是聚类集合$C$。大致思路是：对于每一个子图$sg_i$，选出与它相似度最高的聚类。若小于阈值$\epsilon$，则加入这个聚类；否则新建一个聚类。$\epsilon$是算法的重要参数，根据实验确定。

定义3 （Fregraph）： 给定家族$f$的聚类$c_j \in C$与最小支持度阈值$\theta$，敏感子图$sg=argmax_{sg_i \in c_j} w(sg_i, f)$当其支持度$sup_f(sg)=\frac{|c_j|}{falNum(f)}$不小于$\theta$时，被称为fregraph。

特征建立

为实现恶意软件家族分析，所有属于已知家族的fregraph被嵌入一个特征空间，每个fregraph $fg$被赋予一个加权分数$fs$，代表它对恶意软件家族分析的重要程度。

在某些fregraph属于多个族的情况下，fregraph与族之间存在映射。下图示意了在4个fregraph与3个家族之间的映射关系。fregraph与族之间的数定义为fregraph对其相应族的支持度。属于多个家族的fregraph（如$fg_2$）应该比只属于一个家族的fregraph（如$fg_3$）具有更低的重要性，因为后者提供的信息比前者更有用

4个fregraph与3个家族之间的映射示意图

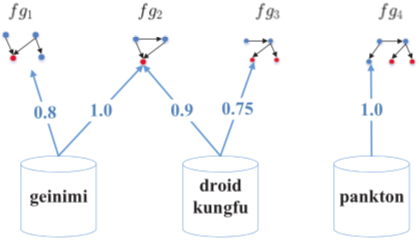
使用下式计算fregraph $fg$的加权分数。
$$
fs(fg) = cb’(fg) * \sum_{f_j \in F} w(fg, f_j) * p(f_j|fg)
$$
其中，$p(f_j|fg)$表示当包含fregraph $fg$时，该应用程序属于家族$f_j$的概率。它使用下式计算：
$$
p(f_j|fg) = \frac{sup_{f_j}(fg)}{\sum_{f_i \in F}sup_{f_i}(fg)}
$$
$cb’(fg)$表示$fg$的归一化熵值。$cb’(fg)$通过下面两式获得，其中$cb_{max}$与$cb_{min}$分别代表相关的最大值与最小值。$cb’(fg)$的区间是0到1，较高的$cb’(fg)$说明$fg$只属于很少的家族。若$cb’(fg)=1$，则$fg$只属于一个的家族。
$$
cb(fg) = \sum_{f_j\in F} p(f_j|fg) * \log{p(f_j|fg)}
$$
$$
cb’(fg) = \frac{cb(fg) - cb_{min}}{cb_{max} - cb_{min}}
$$

FalDroid的使用

为了加速恶意软件分析，文章利用FalDroid将一个新的恶意软件样本分类到它的家族中，并从一个家族中识别出具有代表性的恶意软件样本，从而减少分析工作量。

Android恶意软件家族分类

FalDroid构造了一个基于fregraph的特征向量来表示每个样本。在向量中，每个基于fregraph的特征的默认值为0，当样本中包含该特征时，将其设置为加权分数。对于训练数据集中已知的样本，将其家族标签附加到特征向量上。然后利用不同的机器学习算法对分类器进行训练。然后将一个新的没有家族标签的恶意样本的特征向量放入分类器中，得到一个家族标签。

典型恶意软件样例选取

对于包含过量样本(本文数据集中有1504个样本)的多个家族的每个样本的深入检查是低效的。文章优先检查每个家族的代表性恶意软件样本，以减少分析工作量，加快恶意软件分析。因此，首先构建了一个恶意软件相似图（malware similarity graph，MSG）来描述同一个家族中恶意软件样本之间的关系。

定义3 （MSG）： MSG是一个无向图，对于一个恶意软件家族$f$，$MSG_f = \left{ MV, ME \right}$，其中，

$MV = \left{ \alpha_i | 1 \leq i \leq falNum(f) \right}$，表示家族$f$的恶意软件样本集合，每个节点$\alpha_i \in MV$代表一个恶意软件样本。
$ME$表示边的集合，边$(\alpha_i, \alpha_j)$代表样本$\alpha_i$与$\alpha_j$的相似度大于阈值$\eta$。

一个MSG包含多个群（group），每个群表示MSG中的一个连通子图。MSG中的每个节点只属于一个群。

MSG示意图

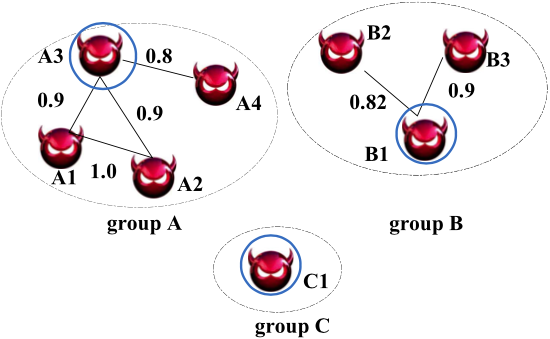
上图是一个有三个群（即群A，B与C）的MSG的示意图，阈值$\eta=0.8$。边旁边标注的数字表示两个节点的相似度。每个恶意软件样本用基于fregraph的特征向量表示。两个样本$\alpha_1$与$\alpha_2$的相似度由它们的向量$\vec{u}$与$\vec{w}$的余弦距离计算出。$\left| \vec{u} \right| = \left| \vec{w} \right| =l$。

$$
sim(\alpha_1, \alpha_2) = \frac{\vec{u} \cdot \vec{w}}{| \vec{u} | | \vec{w} |}
= \frac{\sum_{i=1}^l \vec{u_i}\vec{w_i}} {\sqrt{\sum_{i=1}^l \vec{u_i}^2} \sqrt{\sum_{i=1}^l \vec{w_i}^2}}
$$

对于一个家族中的每一个群，选取与连通节点相似度之和最大的节点作为典型节点，其正式定义为：
$$
\alpha’ = \mathop{argmax}\limits_{\alpha \in GV(group)} \sum_{\beta \in SN(\alpha)} sim(\alpha, \beta)
$$
其中，$GV(group)$表示在$group$中节点的集合，$SN(\alpha)$表示$\alpha$相临节点的集合。上图中，典型节点有A3、B1与C1，用蓝色圆圈标记。只包含一个样本的群（如群C）存在。样本C1不类似于其他样本，因为C1与其他节点的相似性都低于$\eta$。在文章的方法中，C1也被认为是家族中具有代表性的样本，如同A3和B1。

安全分析人员应该关注从每个家族中选择的有代表性的恶意软件样本，而不是所有的恶意软件样本。因此，FalDroid可以减少分析工作量，加快恶意软件分析。

结语

本文使用包括TF-IDF与图分析在内的多种方法，对Android恶意软件进行家族分析，并针对每个家族获取典型样本以简化分析流程。对于家族分析，本文是具有代表性的一篇文章，值得细心一读。