用于细粒度分类的恶意软件可视化
本文介绍2018年发表在IEEE Access的一篇文章,题目是《Malware Visualization for Fine-Grained Classification》,DOI信息在这里。
在这篇文章中,作者首先将恶意软件样本通过一定的方法转化为图像,之后使用计算机视觉领域成熟的识别方法对图像进行分类,不仅识别效果良好,而且可以直观地看到同一家族恶意软件的特征。
摘要
由于自动工具的快速出现,恶意软件变种的数量急剧上升,为互联网安全带来了极大的威胁。近期,快速分析恶意软件的方法被提出,但这些方法通常需要大量的计算开销,并且难以针对大规模、复杂的恶意软件样本集进行准确分类。因此,在本文中,作者提出了一种新颖的可视化方法,全局和局部地对恶意软件进行分析,以便快速有效地实现细粒度分类。作者使用一个新型的方法,将恶意软件可视化为RGB彩色图像,并从图像中提取全局特征。选择灰度共生矩阵(Gray-level co-occurrence matrix,GLCM)与颜色矩(color moment)分别描述全局纹理特征与颜色特征,产生低维度的特征数据,减少模型训练的复杂度。此外,从恶意软件的代码段和数据段中提取一系列特殊的字节序列,通过Simhash将其作为局部特征处理成为特征向量。最后,作者将全局特征与局部特征合并,使用随机森林、K近邻与支持向量机进行恶意软件分类。实验结果显示,针对来自15个家族的7087个样本,文章的方法最高能够达到97.47%的准确率与96.85%的F-measure。颜色特征和局部特征有效地辅助了基于纹理特征的分类,分别使得F-mearuse提高了3.4%与1%。总体上,全局特征与局部特征的结合能够实现低计算消耗的细粒度恶意软件分类。
简介
由于自动生成工具的广泛传播,大量的恶意软件变种快速生成。根据赛门铁克(Symantec)公司在2017年发布的互联网威胁报告,357 Million个恶意软件变种在去年被识别,平均每天1 Million个。变种的数量成为恶意软件分析的一大挑战。
在已有的分析方法中,使用最多的是静态分析与动态分析。静态分析不执行恶意样本,只分析反汇编代码。在静态分析中,研究者使用的典型方法是从反汇编代码中提取操作码(opcode),API序列与函数调用图,作为分析的原始特征。静态分析可以快速捕获语法和语义信息进行深入分析,但这种方法容易受到代码混淆和加密技术的干扰。动态分析一般通过在受监控的虚拟环境中执行样本,分析行为信息,如网络活动、系统调用、文件操作与注册记录修改。它具有更好的鲁棒性,但恶意软件执行的时间与资源消耗是昂贵的。静态分析与动态分析均有各自的优点与缺点,但是考虑动态分析对时间与资源的要求,静态分析在处理大量恶意软件时更有优势。
近年来,基于可视化的方法被提出,以通过直接分析恶意软件二进制文件进行分类,这进一步提高了恶意软件分析的效率,因为不需要深入的分析。这种方法之所以能够很好地工作,是因为大多数变种都是通过使用自动化技术或重用一些重要模块生成的,所以它们在二进制代码中有一些相似之处。但是,目前存在的多数可视化方法基于灰度,通过纹理评估相似性,不能应用于字节均匀分布的恶意软件。此外,几乎所有方法只使用全局特征识别恶意软件,导致分类模型对复杂恶意软件不够稳定,只能应用于少量具有标记图像特征的恶意样本。
因此,在本文中,作者提出一个新颖的可视化方法,将全局特征与局部特征结合,以识别和分类恶意软件。对于全局特征,作者创建了一个新的方法,将恶意软件可视化为RGB着色的图像,从中提取纹理特征与颜色特征。RGB彩色图像能够展示家族之间的相似性,但是对同一家族的变种不够明显。因此,作者将一些可以通过ASCII转换可视化的连续字节值序列视为局部特征,以揭示这些变种的相似性。实验结果显示,该方法结合全局特征和局部特征,具有较高的分类精度和较高的分类性能。文中方法主要提供了一种新的恶意软件可视化方法、一种恶意软件局部特征提取方法和一种恶意软件分类方法,从而在实践中能够对各种复杂的恶意软件实现高效率、高精度处理。
机制概述
文章的方法由三阶段组成:恶意软件可视化、特征提取与恶意软件分类,详细过程如下图所示。在恶意软件可视化阶段,提出一个新颖的RGB彩色图像生成的方法,以解决灰度图像信息不足的问题。作者没有试图寻找将灰度图转化为RGB彩色图的方法,而是在红、绿、蓝三个通道中填充更多有用的信息。字节值可以直接反映恶意软件的性质,但容易发生变化,因此作者增加了恶意软件段(section)的熵值和相对大小,从而增强了恶意软件图像的稳定性。这一方法使得不同段间的差异更加明显,易于分辨其家族,从而有助于分类。为增强方法处理复杂数据集的鲁棒性,作者从代码与数据段中提取局部特征。这一方法只关注能够转化为字符串的连续字节值序列,因为这些字节序列通常代表诸如字符串常量、API调用与DLL的重要信息,因此它们在生成变种时被稳定继承的可能性很大。在特征提取阶段,文章从RGB彩色图中提取全局信息,从软件段中提取局部信息,之后将它们合并。使用灰度共生矩阵提取纹理特征,因为它的计算复杂度比其它算法低。颜色矩是一个简单而有效的方法,用于描述颜色特征。对于图像的局部特征,通常提取点(spot)和角(corner)作为特征点,但这些特征点对于恶意软件来说没有意义。因此,文章选择可以转换为ASCII字符串的字节序列作为局部特征,并将它们排列为特征向量。在最后的分类阶段,选择了三种不同的分类器(随机森林、k近邻与支持向量机)来分类恶意软件。
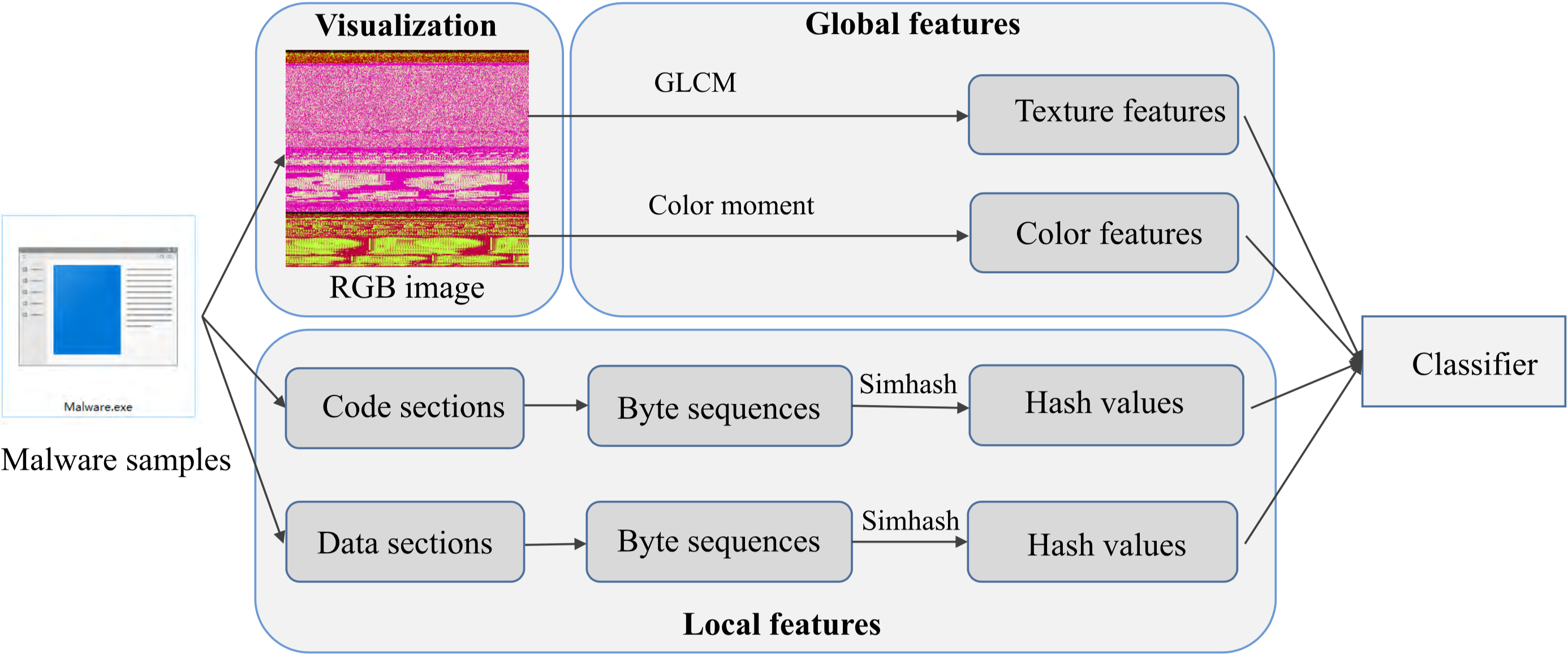
恶意软件可视化及其分类
恶意软件可视化
恶意软件可视化的核心步骤是段划分与特征计算。首先,对恶意代码进行过滤,以确保样本遵循PE格式并保留原始结构。然后,根据PE格式将恶意软件分为多个段,利用熵、字节值和相对大小对这些部分进行特征描述。每个像素的红、绿、蓝通道用这些值填充,最后组合为一个RGB彩色图。详细过程如下图。
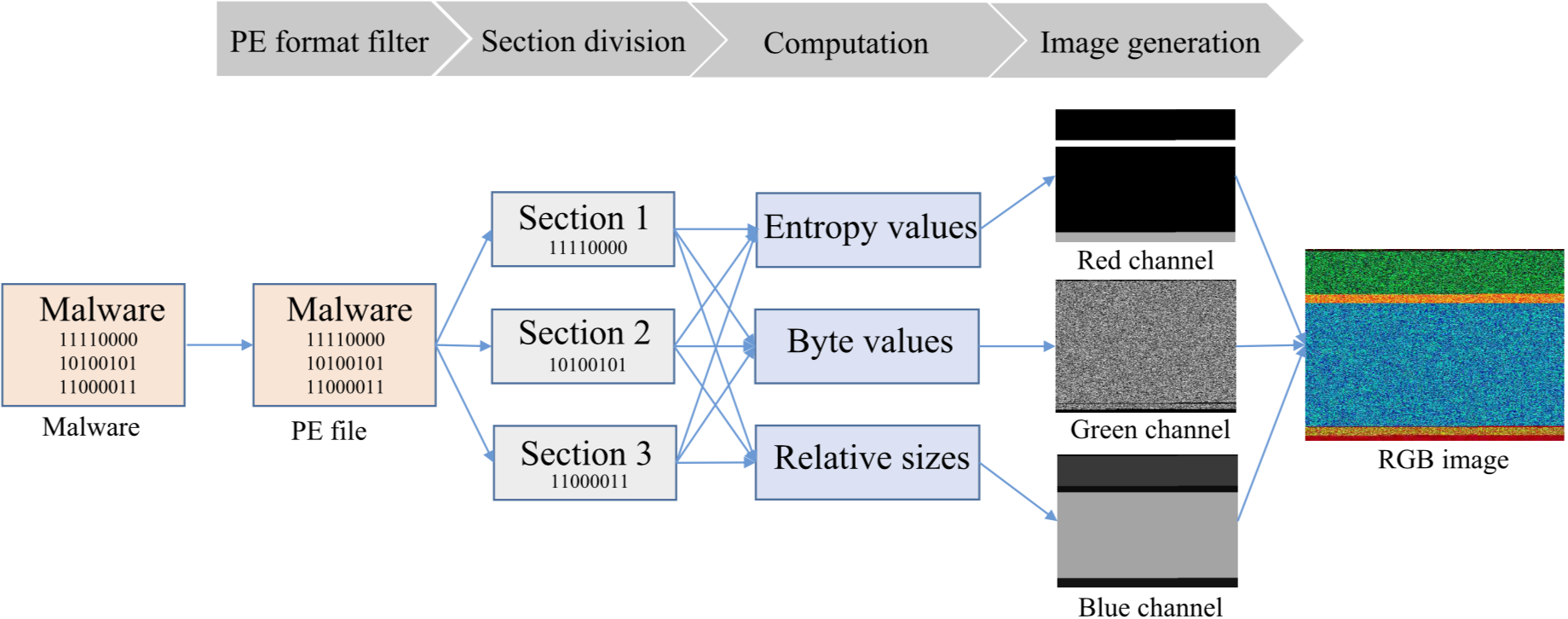
恶意代码过滤是决定方法有效性的先决条件。非PE结构的文件难以划分并保留结构信息,因此它们在文章中暂不考虑。使用PE语法分析器判断恶意软件是否为PE结构。PE文件结构和过滤恶意软件所需的字段信息如下图所示。“e_magic”与“Signature”两个字段需要验证。

在段划分过程中,保留了PE文件原有的段结构。代码段、数据段和其它天然的段仍然被视为完整的部分,但是其余段,如Dos头、PE头和文件末尾的附加数据,则根据它们的位置进行合并。在段划分之后,计算熵和相对大小来表示这些划分,因为它们可以表现出高水平的特征,并反映出恶意软件在总体上的相似性。
熵可以表示段中字节值的混乱程度。当变量变化较小时,它们段的熵几乎相同。熵可以用如下公式计算:
$$
SectionEntropy = -\sum_{255}^{i=0} p(c_i)\log_2 p(c_i)
$$
其中,$p(c_i)$是字节值$i$出现的概率。当段中所有字节值相同时,熵取最小值0;反之,所有字节值不同时,熵取最大值8。0至8是一个很小的范围,用它表示灰度,人眼难以分辨。因此,熵被放大31.875倍,作为红通道的值,以达到更好的可视化效果。
$$
\begin{equation}
\begin{split}
RedComponent &= SectionEntropy \times \frac{255}{8} \
&= (-\sum_{255}^{i=0} p(c_i)\log_2 p(c_i)) \times 31.875
\end{split}
\nonumber
\end{equation}
$$
使用下图所示的方法填充RGB彩色图的绿通道。恶意软件二进制文件由一系列0和1组成。一个字节包含8位(8个二进制数),可以将其转换为0到255之间的小数(字节值)。每个字节值用于表示一个灰色级别(0表示黑色,255表示白色,其他值表示不同程度的灰色)。最后将字节值组织为二维矩阵,并将其可视化为图像。图像的宽度由文件的大小决定,高度也随之改变。大小是描述段的基本方式,但一个段对整个文件的相对大小更适合用于对比。相对大小同样需要扩大255倍,作为蓝通道的像素。
$$
BlueComponent = \frac{SectionSize}{FileSize} \times 255
$$
在提取纹理特征之前,需要将RGB彩色图像转换为灰度图像。在转换过程中,给出红、绿、蓝三种通道的不同比例,相当于为熵、字节值和相对大小分配权重。下面是将RGB颜色转换为灰度的一种著名的转换方法。
$$
Gray = R * 0.299 + G * 0.587 + B * 0.114
$$
其中,$R$、$G$与$B$分别代表红、绿、蓝部分,分别与熵、字节值、相对大小匹配。在序列中的每个字节值应在32与126(十进制)之间,因为这样才可以转化为ASCII字符串。此外,局部特征提取自连续字节序列,因为这些序列包含一些特殊的信息。例如,字符串常量、动态链接库(DLL)名称和系统调用函数名称都是字符串类型,通常通过ASCII转换为二进制,然后存储在代码或数据段中。当恶意软件发生变化时,这些字符串更有可能被保留,并且可以在对来自类似家族的样本进行分类时发挥重要作用。因此,可以将这些序列作为图像显示,并对它们进行比较,以验证局部特征的有效性。为了说明局部特征,文章提出了一种根据字节序列的对应ASCII字符串类型,来进行字节序列可视化的新技术。该方法将字节值分为五个范围,每个范围用一种颜色表示,如下表。为了清楚地显示颜色之间的差异,文章没有使用字节值来控制颜色的深度,只根据ASCII类型确定基本颜色。
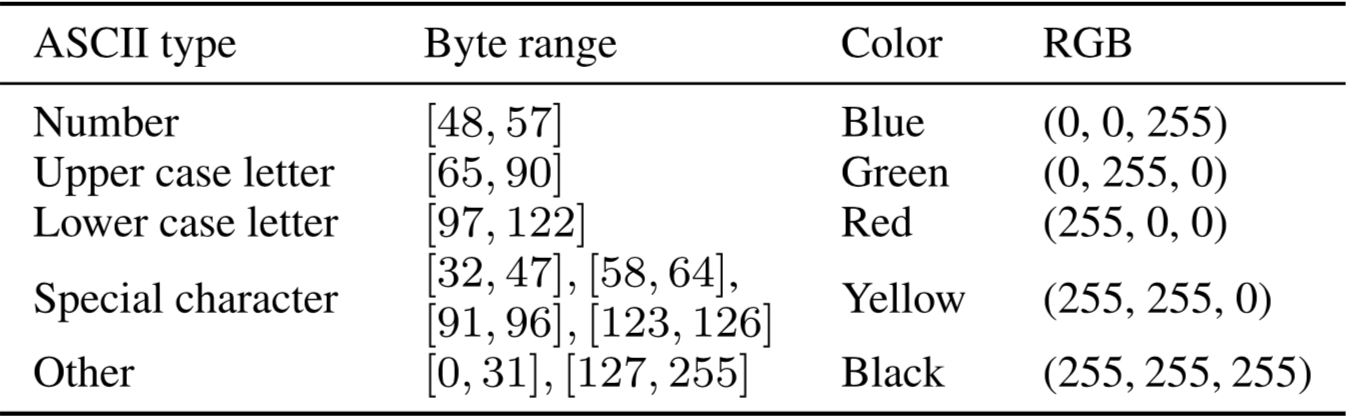
特征提取
全局特征
恶意软件可视化后的下一步是提取特征进行恶意软件分类。图像特征提取一般包括两种方法:一种是从整个图像中提取全局特征;另一种是提取局部特征点,然后用适当的特征描述它们。全局特征通常描述图像的纹理、颜色、形状和空间。通过分析恶意软件图像的特征和包含的信息,文章认为纹理特征和颜色特征作为恶意软件的全局特征更加合适和充分。常用的纹理特征提取算法包括灰度共生矩阵、局部二值模式(Local Binary Pattern,LBP)和Gabor变换,而GLCM最适合文章低计算复杂度的需要。与颜色直方图、颜色集合和颜色相关图相比,颜色矩对颜色分布的表达更有效,特征维数更小,因此选择颜色矩提取颜色特征。
纹理特征
灰度共生矩阵基于图像中像素的空间分布包含图像纹理信息的假设。共生矩阵是图像中两个灰度像素在距离$d$处的联合概率分布。灰度共生矩阵可以从方向、相邻区间、变化幅度等方面反映灰度的综合信息。角度$\theta$、偏移$d$与灰度级是灰度共生矩阵的三个重要参数。灰度共生矩阵的角度为灰度的变化方向,文章选择了四个:$0^\circ$,$45^\circ$,$90^\circ$与,$135^\circ$,包含了纹理变化的主要角度。偏移是两个灰度像素的距离,两个相邻的像素表示它们在给定的方向上,偏移量为1。灰度级实际上是图像中灰度值的最大值加1,它也是灰度压缩中使用的灰度值。GLCM主要包括灰度压缩、共生矩阵生成和特征计算三个步骤。

上图展示了灰度共生矩阵的特征提取过程,其中角度为0度、偏移为1、灰度级为3。首先将RGB彩色图转化为灰度图。采用灰度压缩的方法来减少矩阵维数和计算量。图中,矩阵维度从12×12压缩到4×4,计算量降低了10倍左右。生成共生矩阵的方法是求出每个矩阵元素对应于位置$(i, j)$的像素对个数。这个数应该乘以2,因为它需要从相反的方向重新计算。共生矩阵一般不直接作为纹理特征来处理,因为矩阵的元素太多了。因此Haralick等人提出了14种基于共生矩阵的统计量来表示纹理特征。本文只使用了其中5种,包含角二阶矩(Angular Second Moment,ASM)、熵(Entropy)、对比度(Contrast)、反差分矩阵(Inverse Differential Moment,IDM)与相关度(Correlation)。因此,纹理特征的维数是20(4个方向×5个统计量)。计算公式如下(M为共现矩阵):
角二阶矩(Angular Second Moment,ASM)
$$
ASM = \sum_i \sum_j M(i ,j)^2
$$
ASM是每个矩阵元素的平方和。ASM反映了灰度分布的均匀性和纹理的粗度。如果共生矩阵的所有值都相等,则ASM将很小。否则,如果某些值很大,而另一些值很小,则ASM将很大。较大的ASM代表更均匀和有规律变化的纹理模式。熵(Entropy)
$$
Ent = -\sum_i \sum_j M(i ,j) \log M(i ,j)
$$
熵表示图像中纹理的非均匀性或复杂性的程度。当像素接近随机或者图像有很多噪声时,熵会很大。熵越大,图像越复杂。对比度(Contrast)
$$
Con = \sum_i \sum_j (i - j)^2 M(i ,j)
$$
对比度直接反映一个像素值与其相邻像素值的亮度对比度,表明图像的清晰度和纹理的凹槽深度。纹理凹槽越深,对比度越大,纹理越清晰。相反,对比度越小,凹槽越浅,纹理越模糊。反差分矩阵(Inverse Differential Moment,IDM)
$$
IDM = \sum_i \sum_j \frac{M(i ,j)}{1 + (i - j)^2}
$$
IDM反映了图像纹理的同质性,度量了图像纹理的局部变化。大的IDM表明图像的不同区域之间没有变化,局部均匀性一定很高。而如果共生矩阵对角线上的元素包含一个较大值,IDM将取一个较大的值。相关度(Correlation)
$$
\begin{equation}
\begin{split}
Corr &= \sum_i \sum_j \frac{(i, j)M(i, j) - \mu_i \mu_j}{s_i s_j} \
\mu_i &= \sum_i \sum_j i \cdot M(i, j) \
\mu_j &= \sum_i \sum_j j \cdot M(i, j) \
s_i^2 &= \sum_i \sum_j M(i, j) (i - \mu_i)^2 \
s_j^2 &= \sum_i \sum_j M(i, j) (j - \mu_j)^2 \
\end{split}
\nonumber
\end{equation}
$$
相关度反映纹理的方向,表示灰度值沿一定方向的延伸长度,常用来评估共生矩阵中行元素与列元素的相似性。灰度扩展越长,相关度越大。
颜色特征
颜色矩是一种简单有效的颜色特征表示方法,通常包括一阶矩(均值,mean)、二阶矩(方差,viarance)和三阶矩(斜度,skewness)等,由于颜色信息主要分布于低阶矩中,所以用一阶矩、二阶矩和三阶矩足以表达图像的颜色分布。与其它描述颜色特征和方法对比,颜色矩不需要颜色空间量化,且特征向量维数低。图像的颜色矩总共只产生9个分量(3个色阶分量,每个分量3个低阶矩)。矩的具体公式如下:
一阶矩
$$
\mu_i = \frac{1}{N} \sum_{j=1}^N p_{i,j}
$$二阶矩
$$
\sigma_i = ( \frac{1}{N} \sum_{j=1}^N ( p_{i,j} - \mu_i )^2 )^{\frac{1}{2}}
$$三阶矩
$$
s_i = ( \frac{1}{N} \sum_{j=1}^N ( p_{i,j} - \mu_i )^3 )^{\frac{1}{3}}
$$
其中,$N$是图像中像素的数量,$p_{i,j}$是第$i$个颜色通道的第$j$个像素,$\mu_i$表示第$i$个颜色通道所有像素的均值,$\sigma_i$表示第$i$个颜色通道所有像素的标准差,$s_i$表示第$i$个颜色通道所有像素斜度的立方根,一阶矩反映图像的亮度,二阶矩反映颜色分布的范围,三阶矩反映颜色分布的对称性。红、绿、蓝三个分量的色矩构成一个9维向量,表示为:
$$
F_{color} =[ \mu_R, \sigma_R, s_R,\mu_G, \sigma_G, s_G, \mu_B, \sigma_B, s_B ]
$$
局部特征
在提取局部特征之前,需要获取代码段和数据段。由于PE文件的段名不同,文章将包含“.text”、“CODE”与“.code”的部分叫做代码段,包含“.data”、“.rdata”、“.idata”与“.edata”的部分叫做数据段。然后提取字节序列,将字节序列转换为ASCII字符串(字节范围为32到126),用Simhash将它们处理为特征向量。Simhash在2002年由Charikar提出,被Google用于删除数亿个网页的重复。这种哈希方法确保了类似的文本在哈希之后仍然具有相似性,并极大地减少了数据维度。Simhash是一种局部敏感哈希 (Locality Sensitive Hash,LSH)。它的主要思想是降维,将高维特征向量映射为低维特征向量,并保持相似性。两个向量的汉明距离(Hamming Distance)通常用于测量相似度。文章的方法不需要计算汉明距离,直接使用最后生成的特征向量作为局部特征。提取和处理局部特征的详细过程包括五个步骤,如下所述:
- 提取连续字节值序列,序列中的每个字节值都可以转换为ASCII字符(字节值在[32,126]范围中)。序列的长度用作序列的权重。
- 使用传统的哈希算法(如MD5)对每个序列进行哈希,生成一个0和1的$n$比特向量。哈希算法必须保证不同序列的哈希值是不同的。
- 为向量中的每个元素$S_i$赋权。若$S_i$为0,则赋权结果取负数$-W_i$,反之若$S_i$为1,则赋权结果取正数$W_i$。
- 对于所有加权向量,元素根据它们的位置被合并为一个$n$比特向量。
- 遍历累积结果的所有元素,如果元素大于0,则在相应的位置取1,否则取0。最后得出的结果是一个特征向量,作为局部特征。
下图是构造局部特征的一个示例。一系列连续的字节值$n$($32\leq n\leq 126$)被视为恶意软件的一个关键的部分,如同图像处理中的局部特征点。序列越长,就越有可能位于局部的稳定区域(例如文件路径、电子邮件地址),因此相应的权重应该更大。根据哈希值元素的1或0选择的加权结果加上或减去相应的权重。最后的特征向量是一个由0和1组成的n比特向量,通过加权结果进行转换。$n$由传统的哈希方法确定。在文章的方法中,作者使用64位MD5作为哈希算法,因此局部特征的维度为128(数据部分为64,代码部分为64)。
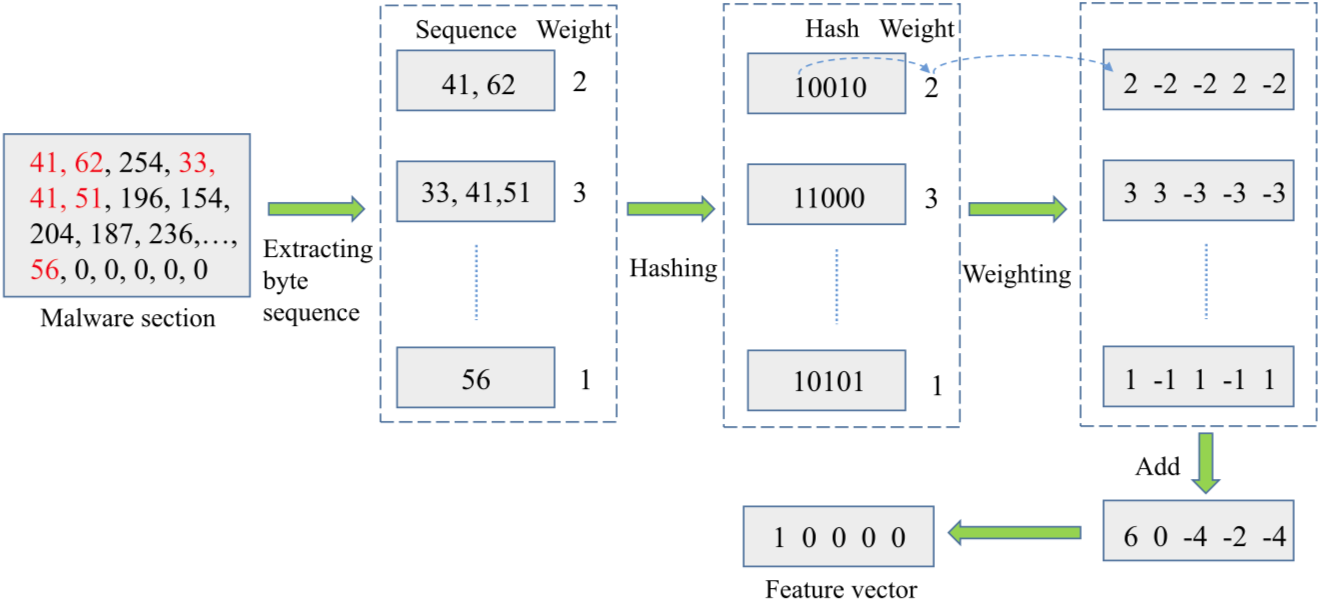
结语
本文采用图像处理的方法,结合恶意代码检测,完成了具有创新性的工作,十分新颖。其中涉及图像特征提取的相关内容,需要认真学习。